练习册

  • 练习册
  • 试题

    河北省邯郸市2009年高三年级第一次模拟考试       

    数学（文史类）

    本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分　第Ⅰ卷1至2页　第Ⅱ卷3至4页　考试结束后，将本试卷和答题卡一并交回　

    第Ⅰ卷（选择题60分）

    注意事项：

    1　答题前，考生在答题卡上务必用直径0　5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码　请认真核准条形码上的准考证号、姓名和科目　

    2　每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效　

    3　本卷共12小题，每小题5分，共60分　在每小题给出的四个选项中，只有一项是符合题目要求的　

    参考公式：

    如果事件高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。互斥，那么                                   球的表面积公式

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                                    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                                    

    如果事件高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。相互独立，那么                            其中高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。表示球的半径

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。                                         球的体积公式

    如果事件高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在一次试验中发生的概率是高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，那么          高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。次独立重复试验中事件高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。恰好发生高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。次的概率           其中高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。表示球的半径

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    一、             选择题（本大题共12个小题．每小题5分；共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）

    1．设高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。,高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。,高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。则高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                   

    试题详情

    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。      高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    2. 在等差数列高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。中，已知高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，则高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的值为

    试题详情

    A．高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。               B．高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。           C．高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。             D．高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    3.若ABCD为平行四边形，E是CD的中点，则高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。等于

    试题详情

    A．高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。      B. 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。    C. 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。   D.高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    4．下列函数中，在高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。上是偶函数的是                                      

    试题详情

         A. 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。        B. 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。      C. 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。       D.高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    5.已知函数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

           A．－高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                       B． 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                   C．2                         D．－2

    试题详情

    6. 已知函数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的图像与函数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的图像关于直线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。对称，则高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的解析式为

    试题详情

    A.高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。                B.高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。 

    试题详情

    C.高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。               D.高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    7. 棱长为a的正四面体中，高为h，斜高为m，相对棱间的距离为d，则a、m、h、d的大小关系正确的是         

           A．a＞m＞h＞d                                    B．a＞h＞m＞d

    C．a＞h＞d＞m                        D．a＞d＞h＞m

    8某学校共有教师490人，其中不到40岁的有350人，40岁及以上的有140人.为了了解普通话在该校中的推广普及情况，用分层抽样的方法，从全体教师中抽取一个容量为70人的样本进行普通话水平测试，其中在不到40岁的教师中应抽取的人数为      

    A    20              B   40            C  50           D   60

    试题详情

    9.以直线高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。和高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。为渐近线的双曲线的离心率为

    试题详情

    A. 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。               B. 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。             C.  高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。        D. 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    10．设函数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。若高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，则x0的取值范围是       

        A．（－1，1）                       B．（－1，+∞）

        C．（－∞，－2）∪（0，+∞）        D．（－∞，－1）∪（1，+∞）

    试题详情

    11.高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的一边AB上有4个点，另一边AC上有5个点，连同 高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的顶点共10个点，以这些点为顶点，可以构成三角形的个数是  

    A. 120               B. 90               C. 100            D. 60

    试题详情

    12  在一个局部环境中，人口数量高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。随时间高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的增长通常遵循逻辑斯谛（Logistic）增长曲线,如图所示，由该图可以得出如下判断：

    试题详情

    ①在高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。内，人口增长越来越快，在高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。上人口增长越来越慢；

    试题详情

    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。②在高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。内，人口增长越来越慢，在高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。上人口增长越来越快；

    试题详情

    ③在高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。时，人口增长最快，随着时间的推移，人口数量将趋于平稳值高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。；

    试题详情

    ④在高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。时，人口增长最慢，随着时间的推移，人口数量将趋于平稳值高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。.

    上述判断正确的是                                      

    A   ①③          B ①④             C   ②③            D ②④

     

     

    第Ⅱ卷（非选择题90分）

     

    试题详情

    二、填空题(本大题共4小题，每小题5分，共20分)

    13.高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的展开式中含x的正整数指数幂共有              项;

    试题详情

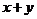    14.已知变量x、y满足条件高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。则高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的最大值是        ;

    试题详情

    15. 抛物线的顶点在原点，焦点在y轴上，抛物线上一点P（m,－3）到焦点的距离为5，则抛物线的方程是           ;

    试题详情

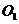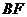    16. 两个边长分别为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的全等矩形高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。和高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。依等边高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。拼接为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的二面角，设高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。中点为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。中点为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。中点为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，则三角形高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的面积为      .

    试题详情

    三、解答题（本大题共6小题，共70分　解答应写出文字说明，证明过程或演算步骤）　

    17．（本小题满分10分）

    试题详情

    已知函数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。.求:

    试题详情

        (I) 函数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的最大值及取得最大值的自变量高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的集合；

    试题详情

    (II) 函数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。在高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的单调减区间.

     

     

     

     

    试题详情

    18．（本小题满分12分）

       一个盒子装有3个白球，3个黑球，

       (I)  现从盒子中任取两个小球，求两球颜色相同的概率；

       (II) 现从盒子中逐一摸取小球，且每次取出后均不放回，若取到黑球则停止抽取，否则继续进行，求抽取次数不多于三次的概率.

     

     

     

     

     

     

     

     

    试题详情

    19．（本小题满分12分）

    如图，已知四棱锥P－ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，

    AB＝AD＝1，BC＝2，又PB⊥平面ABCD，且PB＝1，点E在棱PD上，且DE＝2PE．

    试题详情

    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。（Ⅰ）求异面直线PA与CD所成的角的大小；

    （Ⅱ）求证：BE⊥平面PCD；

    （Ⅲ）求二面角A－PD－B的大小．

     

     

     

     

     

     

     

    试题详情

    20．（本小题满分12分）

    试题详情

    已知数列高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的首项高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。前高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。项和为高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，且高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

    试题详情

    （I）求数列高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的通项公式；

    试题详情

    （II）令高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，求数列高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的前n项和高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。.

     

     

     

     

     

     

     

    试题详情

    21．（本小题满分12分）

    试题详情

    已知函数高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。，（高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。）求：

    试题详情

    （I）过高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。点且与高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。图像相切的切线方程；

    试题详情

    （II）高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。的单调区间和极值.

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

     

    试题详情

    22．（本小题满分12分）

    试题详情

    如图，M、N是椭圆高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。=1上异于右顶点A的两点,并且高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。.

       （I）若直线AM斜率为k，求点M的坐标；

       （II）问直线MN是否过一定点，如果经过，则求出该点；否则说明理由.

    试题详情

    高考资源网(www.1010jiajiao.com)，中国最大的高考网站，您身边的高考专家。

     

     

     

     

     

     

     

     

     

     

    试题详情

    一、选择题1B  2D  3B   4C  5A  6D  7A  8C  9C  10D  11B  12 A

    二、填空题13、    2    ；  14、   6    ；15、高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 16、高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。或 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    三、解答题

    17．（10分）

    解：（I）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。,即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时, 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。取得最大值高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.

    函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的取得最大值的自变量高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的集合为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………5分

     (II)高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。由题意得: 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    即 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。又由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。因此函数高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的单调减区间为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.……10分

    18.（12分）

    解：（I）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 …………………………4分

    (II)由已知抽取一次停止的概率为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。， ………………6分

        抽取两次停止的概率为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，………………………………………8分

        抽取三次停止的概率为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，………………………………10分

    所以抽取次数不多于三次的概率高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。…………12分

    19.（12分） 解：（Ⅰ）取BC中点F，连结AF，则CF＝AD，且CF∥AD，

    ∴四边形ADCF是平行四边形，∴AF∥CD，

    ∴∠PAF（或其补角）为异面直线PA与CD所成的角　………………………  2分

    ∵PB⊥平面ABCD，∴PB⊥BA，PB⊥BF．

    ∵PB＝AB＝BF＝1，∴AB⊥BC，∴PA＝PF＝AF＝高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．　

    ∴△PAF是正三角形，∠PAF＝60°

    即异面直线PA与CD所成的角等于60°．　……………4分

    （Ⅱ）在Rt△PBD中，PB＝1，BD＝高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，∴PD＝高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。∵DE＝2PE，∴PE＝

     

     

     

    则高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，∴△PBE∽△PDB，∴BE⊥PD．　……………………     5分

    由（Ⅰ）知，CF＝BF＝DF，∴∠CDB＝90°．

    ∴CD⊥BD．又PB⊥平面PBD，∴PB⊥CD．

    ∴CD⊥平面PBD，∴CD⊥BE　………………………………7分

    ∴BE⊥平面PCD．　…………………………………………8分

    （Ⅲ）连结AF，交BD于点O，则AO⊥BD．

    ∵PB⊥平面ABCD，∴平面PBD⊥平面ABD，∴AO⊥平面PBD．

    过点O作OH⊥PD于点H，连结AH，则AH⊥PD．

    ∴∠AHO为二面角A－PD－B的平面角．　…………………………………     10分

    在Rt△ABD中，AO＝．

    在Rt△PAD中，AH＝高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．　

    在Rt△AOH中，sin∠AHO＝高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。．

    ∴∠AHO＝60°．            

    即二面角A－PD－B的大小为60°．　………………………………………      12分

    20.（12分） 解：（Ⅰ）由已知高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。可得当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    两式相减得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，从而高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，所以 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    所以有 高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    故总有高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，又高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。从而高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。；………6分

    （II）由（I）知高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    因为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。=高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    =高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。-高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    记高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，由错位减法，可得

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………10分

    故高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 ……………12分

    21.(12分) 解：（Ⅰ）高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    因为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。点在高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的图像上，

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为切点时，切线的斜率高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    此时过点高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的切线方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。；……………2分

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。不是切点时，若切线存在，则切线的斜率k存在，设切点为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……………4分

    可设切线方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，由于切点高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在切线上，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。①

    又切点高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在曲线上，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。②

    联立①②解得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。所以另一条切线方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。………6分

    （II）由高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。可得高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。和高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，故高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的单调递减区间为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。和高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。；单调递增区间为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。；且高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。 ……………12分

    22.解：（Ⅰ）依题意，直线 AM方程为：y=k(x－2)，高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    易知点M的横坐标高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    从而点M坐标为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.…………6分

       （II）①当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，易求直线高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。……8分

     

    ②当高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，

    ∵AM⊥AN，故AN方程：高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，同理可求出N点坐标，

            高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

            高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。………………10分

            MN直线方程为高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

            化简为：高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    即高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

     综上，MN直线恒过定点（高考资源网(www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，0）.……………………………………12分

     

     

     


    同步练习册答案