
2009云南省曲靖一中高考冲刺卷文科数学(七)

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)

一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只
有一项是符合题目要求的
1.设全集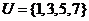 ,集合
,集合 ,则
,则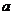 的值为
的值为
A.3 B.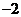 D.
D.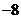

2.不等式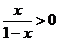 的解集是
的解集是
A.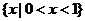 B.
B.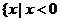 或
或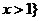

C.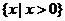 D.
D.

3.设点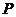 的坐标为
的坐标为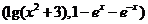 ,则点
,则点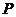 位于
位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.设直线 ,则
,则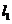 到
到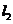 的角是
的角是
A.30° B.60° C.120° D.150°
5.设函数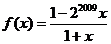 ,那么
,那么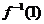 的值等于
的值等于
A.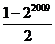 B.
B.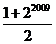 C.0 D.
C.0 D.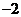

6.不等式组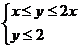 ,所表示的平面区域的面积是
,所表示的平面区域的面积是
A.1 B.


7.若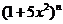 的展开式中各项系数之和是
的展开式中各项系数之和是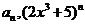 的展开式中各项的二项式系数之
的展开式中各项的二项式系数之
和是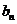 ,则数列
,则数列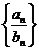 为
为
A.公差为2的等差数列 B.公差为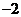 的等差数列
的等差数列
C.公比为 的等比数列 D.公比为3的等比数列
的等比数列 D.公比为3的等比数列
8.设曲线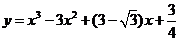 在
在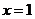 处的切线的倾斜角为
处的切线的倾斜角为 ,则
,则 的取值是
的取值是
A. B.
B.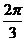 C.
C.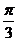 D.
D.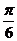

9.函数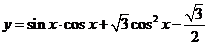 的图象的一个对称中心是
的图象的一个对称中心是
A. B.
B.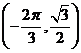 C.
C.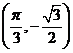 D.
D.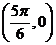

10.某单位购买10张北京奥运会某场足球比赛门票,其中有3张甲票,其余为乙票.5名
职工从中各抽1张,至少有1人抽到甲票的方法数是
A.231 B.
11.已知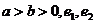 分别是圆锥曲线
分别是圆锥曲线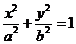 和
和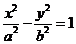 的离心率,设
的离心率,设
 ,则
,则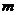 的取值范围是
的取值范围是
A.(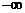 ,0) B.(0,
,0) B.(0,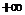 ) C.(
) C.(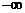 ,1) D.(1,
,1) D.(1,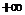 )
)
12.在半径为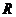 的球
的球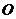 内有一内接正三棱锥
内有一内接正三棱锥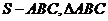 的外接圆恰好是球
的外接圆恰好是球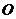 的一个
的一个
大圆,一个动点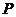 从顶点
从顶点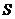 出发沿球面运动,经过其余三点
出发沿球面运动,经过其余三点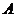 、
、 、
、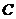 后返回点
后返回点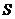 ,
,
则点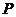 经过的最短路程是
经过的最短路程是
A.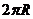 B.
B.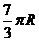 C.
C.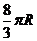 D.
D.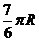


第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.已知向量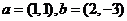 ,若
,若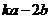 与
与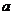 垂直,则实数
垂直,则实数 .
.
14.若等比数列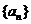 中,
中,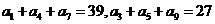 ,则数列
,则数列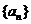 的前9项和
的前9项和
 .
.
15.已知点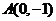 及直线
及直线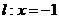 ,点
,点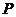 是抛物线
是抛物线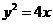 上一动点,则点
上一动点,则点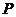 到定点
到定点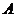 的
的
距离与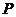 到直线
到直线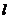 的距离和的最小值为
.
的距离和的最小值为
.
16.已知平面 、
、 、
、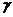 及直线
及直线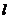 、
、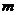 满足:
满足: ,那么在
,那么在
结论:① 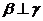 ;②
;② 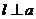 ;③
;③ 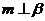 中,可以由上述已知条件推出的结论
中,可以由上述已知条件推出的结论
有
。(把你认为正确的结论序号都填上)
三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
已知角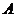 、
、 、
、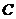 为
为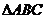 的内角,其对边分别为
的内角,其对边分别为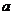 、
、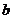 、c,若向量
、c,若向量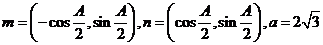 ,且
,且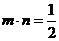 ,
,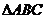 的面积
的面积 ,求
,求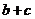 的值.
的值.

18.(本小题满分12分)
甲、乙、丙三人独立解答某一道数学题,已知三人独立解出的概率依次为0.6,0.5,0.5,求:
(1)只有甲解出的概率;
(2)只有1人解出的概率.



19.(本小题满分12分)
设数列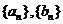 满足:
满足: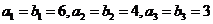 ,且数列
,且数列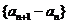 是等差数列,
是等差数列, 是等比数列,其中
是等比数列,其中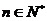 .
.
(1)求数列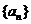 和
和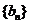 的通项公式;
的通项公式;
(2)求数列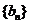 的前
的前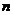 项和
项和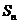 .
.
20.(本小题满分12分)
如图,在直三棱柱中,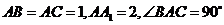 ,
, 为棱
为棱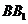 的中点.
的中点.
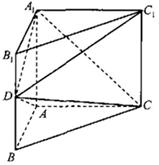 (1)求证:平面
(1)求证:平面 平面
平面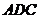 ;
;
(2)求直线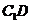 与平面
与平面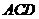 所成角的正切值.
所成角的正切值.






21.(本小题满分12分)
中心在原点,焦点在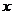 轴上的一椭圆与一双曲线有共同的焦点
轴上的一椭圆与一双曲线有共同的焦点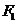 、
、 ,且
,且 ,椭圆的长半轴长与双曲线的实半轴长之差为4,离心率之比为3:7.
,椭圆的长半轴长与双曲线的实半轴长之差为4,离心率之比为3:7.
(1)求两曲线的方程;
(2)设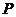 是两曲线的一个交点,求向量
是两曲线的一个交点,求向量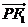 与
与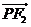 的夹角的余弦值.
的夹角的余弦值.




22.(本小题满分12分)
已知函数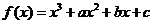 在
在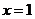 处有极值,
处有极值,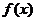 在
在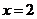 处的切线
处的切线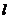 不过第四象限且倾斜角为
不过第四象限且倾斜角为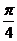 ,坐标原点
,坐标原点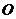 到切线
到切线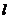 的距离为
的距离为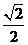 .
.
(1)求切线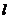 的方程及
的方程及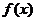 的表达式;
的表达式;
(2)求函数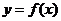 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.

一、
1.B 2.A 3.D 4.A 5.C 6.A 7.D 8.B 9.D 10.A 
11.A 12.B
1.由题意知 ,解得
,解得 .
.
2.由 得
得 ,化得
,化得 ,解得
,解得 .
.
3. ,又
,又 .
.
4.设 到
到 的角为
的角为 的斜率
的斜率 的斜率
的斜率 ,
,
则 ,于是
,于是 .
.
5.由条件,解 即
即 得
得 ,则
,则 .
.
 6.不等式组化得
6.不等式组化得 

平面区域如图所示,阴影部分面积:
 .
.
7.由已知得 ,而
,而
 ,则
,则 是以3为公比的等比数列.
是以3为公比的等比数列.
8. 即
即 ,于是
,于是 ,而
,而 解得
解得 .
.
9.函数可化为 ,令
,令 ,
,
可得其对称中心为 ,当
,当 时得对称中心为
时得对称中心为 .
.
10. .
.
11.由条件得: ,则
,则 得
得 所以
所以 .
.
12.沿球面距离运动路程最短,最短路程可以选
 .
.
二、填空题
13.
 ,由
,由 与
与 垂直得
垂直得 .即
.即
 ,解得
,解得
14.99
在等差数列 中,
中, 也是等差数列,由等差中项定理得
也是等差数列,由等差中项定理得 .
.
所以 .
.
15.
由题意知,直线 是抛物线
是抛物线 的准线,而
的准线,而 到
到 的距离等于
的距离等于 到焦点
到焦点 的距离.即求点
的距离.即求点 到点
到点 的距离与到点
的距离与到点 的距离和的最小值,就是点
的距离和的最小值,就是点 与点
与点 的距离,为
的距离,为 .
.
16.②

一方面.由条件, ,得
,得 ,故②正确.
,故②正确.
另一方面,如图,在正方体 中,把
中,把 、
、 分别记作
分别记作 、
、 ,平面
,平面 、平面
、平面 、平面
、平面 分别记作
分别记作 、
、 、
、 ,就可以否定①与③.
,就可以否定①与③.
三、解答题
17.解: ,且
,且
 ,即
,即
又 .
.


由余弦定理,
 ,故
,故 .
.
18.解:(1)只有甲解出的概率: .
.
(2)只有1人解出的概率: .
.
19.解:(1)由已知 ,∴数列
,∴数列 的公比
的公比 ,首项
,首项


又数列 中,
中,
∴数列 的公差
的公差 ,首项
,首项





∴数列 、
、 的通项公式依次为
的通项公式依次为 .
.
(2) ,
,




 .
.
20.(1)证明;在直三棱柱 中,
中,
 面
面
又

 面
面 ,而
,而 面
面 ,
,
∴平面 平面
平面
(2)解:取 中点
中点 ,连接
,连接 交
交 于点
于点 ,则
,则 .
.
 与平面
与平面 所成角大小等于
所成角大小等于 与平面
与平面 所成角的大小.
所成角的大小.
取 中点
中点 ,连接
,连接 、
、 ,则等腰三角形
,则等腰三角形 中,
中, .
.
又由(1)得 面
面 .
.
 面
面
 为直线
为直线 与面
与面 所成的角
所成的角
又
 ,
,
∴直线 与平面
与平面 所成角的正切值为
所成角的正切值为 .
.
(注:本题也可以能过建立空间直角坐标系解答)
21.解:(1)设椭圆方程为 ,双曲线方程为
,双曲线方程为
 ,半焦距
,半焦距
由已知得 ,解得
,解得 ,则
,则
故椭圆及双曲线方程分别为 及
及 .
.
(2)向量 与
与 的夹解即是
的夹解即是 ,设
,设 ,则
,则
由余弦定理得 ①
①
由椭圆定义得 ②
②
由双曲线定义得 ③
③
式②+式③得 ,式②
,式② 式③得
式③得
将它们代入式①得 ,解得
,解得 ,所以向量
,所以向量 与
与 夹角的余弦值为
夹角的余弦值为 .
.
22.解(1)由 得
得 在
在 处有极值
处有极值
 ①
①
又 在
在 处的切线的倾斜角为
处的切线的倾斜角为
 ②
②
由式①、式②解得
设 的方程为
的方程为
∵原点 到直线
到直线 的距离为
的距离为 ,
,
解得 .
.
又 不过第四象限,
不过第四象限, .
.
所以切线 的方程为
的方程为 .
.
切点坐标为(2,3),则 ,
,
解得
 .
.
(2)

 在
在 上递增,在
上递增,在 上递减
上递减
而
 在区间
在区间 上的最大值是3,最小值是
上的最大值是3,最小值是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com