|
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
6.下列说法错误的是 ( )
试题详情
试题详情
试题详情
试题详情
试题详情
7.将A、B、C、D四个球放入编号为1,2,3的三个盒子中,每个盒子中至少放一个球且A、B两个球不能放在同一盒子中,则不同的放法有
( ) 试题详情
A.15
B.18 C.30 D.36  试题详情
试题详情
试题详情
试题详情
试题详情
曲线的一个交点,若 ,则 ,则 的值为
( ) 的值为
( ) 试题详情
试题详情
试题详情
试题详情
试题详情
第II卷(共100分) 试题详情
 二、填空题:本大题共7小题,每小题4分,共28分. 二、填空题:本大题共7小题,每小题4分,共28分.
11.复数 化简后的结果为
. 化简后的结果为
. 试题详情
试题详情
试题详情
13.“神七”问天,举国欢庆.据科学计算,运载“神舟七号”飞船的“长征二号”系列火箭,在点火1分钟通过的路程为2km,以后每分钟通过的路程增加2km,在到达离地面240km的高度时,火箭与飞船分离,则这一过程大约需要的时间是___________分钟.  试题详情
14.设二项式 展开式中常数项的值为
. 展开式中常数项的值为
. 试题详情
试题详情
试题详情
17.已知 都是负实数,则 都是负实数,则 的最小值是
. 的最小值是
. 试题详情
试题详情
已知函数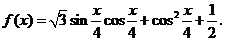 试题详情
(1)求 的单调递增区间; 的单调递增区间; 试题详情
(2)在△ABC中,角A、B、C的对边分别是 ,满足 ,满足 求函数 求函数 的取值范围. 的取值范围. 试题详情
19.(本小题满分14分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为 .现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的,用 .现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的,用 表示取球终止时所需要的取球次数. 表示取球终止时所需要的取球次数. (1)求袋中原有白球的个数; 试题详情
(2)求随机变量 的分布列及数学期望 的分布列及数学期望 ; ; (3)求甲取到白球的概率。 试题详情
试题详情
试题详情
(1)求数列 的通项公式; 的通项公式; 试题详情
(2)求数列 的通项公式; 的通项公式; 试题详情
(3)求证: . . 试题详情
21.(本小题满分15分)已知曲线C上的动点 满足到点 满足到点 的距离比到直线 的距离比到直线 的距离小1. 的距离小1. (1)求曲线C的方程; 试题详情
试题详情
(?) ;(?)点 ;(?)点 总在某定直线上. 总在某定直线上. 试题详情
试题详情
试题详情
(2)求证: ( ( ). ). 2008学年杭州二中高三年级第二学期数学试卷(理科) 试题详情
一、选择题 题号 1 2 3 4 5 6 7 8 9 10 答案 C C A C D D C B A B 二、填空题 11.  ;
12. ;
12.  (或 (或 ); 13. 15;
14. 6; ); 13. 15;
14. 6; 15.  16. 16.  ;
17. ;
17.   三、解答题 三、解答题

 …………12′ …………12′
 故函数 故函数 的取值范围是 的取值范围是 …………12′ …………12′
19. 解:(1)设袋中原有n个白球,由题意知: ,所以 ,所以 =12, =12, 解得n=4(舍去 ),即袋中原有4个白球;
…………4′ ),即袋中原有4个白球;
…………4′ (2)由题意, 的可能取值为1,2,3,4 的可能取值为1,2,3,4   所以,取球次数 所以,取球次数 的分布列为: 的分布列为:

1 2 3 4 P 



  …………9′ …………9′
 (Ⅲ)因为甲先取,所以甲只有可能在第1次和第3次取球,记“甲取到白球”的事件为A, (Ⅲ)因为甲先取,所以甲只有可能在第1次和第3次取球,记“甲取到白球”的事件为A,
 则 则 或 “ 或 “ =3”),所以 =3”),所以 …………14′ …………14′
20. 解:⑴由条件得: ∴ ∴ ∵ ∵ ∴ ∴ ∴ ∴ 为等比数列∴ 为等比数列∴ …………4′
…………4′ ⑵由 得 得  又 ∴ ∴  …………9′
⑶∵ …………9′
⑶∵  (或由 即 即 ),∴ ),∴ 为递增数列. 为递增数列.
∴ 从而 从而 ∴  …………14′ …………14′ 21.解:(1)依题意有 ,由显然 ,由显然 ,得 ,得 ,化简得 ,化简得 ;
…………5′ ;
…………5′ (2)证明:(?)   
 …………10′
…………10′
(?)设点A、B的坐标分别为 ,不妨设点A在点P与点B之间,点 ,不妨设点A在点P与点B之间,点 ,依(?)有 ,依(?)有 *,又可设过点P(2,4)的直线方程为 *,又可设过点P(2,4)的直线方程为 ,得 ,得 , ,  ,代入上*式得 ,代入上*式得
 ,又 ,又 ,得 ,得
 ,当直线AB的斜率不存在时,也满足上式.即点Q总过直线 ,当直线AB的斜率不存在时,也满足上式.即点Q总过直线 ,得证.
…………15′ ,得证.
…………15′ 22. 解:(Ⅰ)设 与 与 在公共点 在公共点 处的切线相同. 处的切线相同. , , ,由题意 ,由题意 , , .即 .即 由 由 得: 得: ,或 ,或 (舍去).即有 (舍去).即有 .
…………4′ .
…………4′ 令 ,则 ,则 .于是当 .于是当 ,即 ,即 时, 时, ; ; 当 ,即 ,即 时, 时, .故 .故 在 在 为增函数,在 为增函数,在 为减函数,于是 为减函数,于是 在 在 的最大值为 的最大值为 .
…………8′ .
…………8′ (Ⅱ)设 则  .故 .故 在 在 为减函数,在 为减函数,在 为增函数,于是函数 为增函数,于是函数 在 在 上的最小值是 上的最小值是 .故当 .故当 时,有 时,有 ,即当 ,即当 时, 时, .
…………15′ .
…………15′
| 






 ,那么集合
,那么集合 中
( )
中
( )


 都在直线
都在直线 上,那么在数列
上,那么在数列 中有
( )
中有
( )
 B.
B. C.
C. D.
D.

 3.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为
( )
3.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为
( )
