
组合数的两个性质
作者:万连飞
教学目的:
1. 使学生掌握组合数的两个性质及其证明方法,培养学生的逻辑思维能力;
2. 使学生能利用组合数的性质进行计算,培养学生的计算能力。
教学过程:
一、复习提问:
1. 组合数公式的两种形式是什么:
2. 利用组合数的公式的第二种形式计算 ,根据学生的回答,教师板书如下:
(1) 组合数公式:
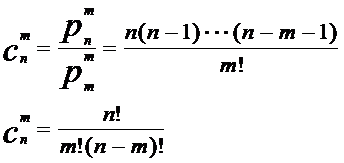 } (n,m∈N,且m≤N)
} (n,m∈N,且m≤N)
二、新课讲授:
1. 通过具体的实例,丰富学生对性质1的感性认识,并加以证明,再讲它的应用。
(1) 利用组合数的公式,考察:
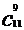 与
与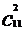 ,
, 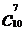 与
与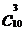 ,
,
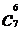 与
与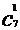
的关系,并能发现什么规律?(可以逐个叫学生回答,板书)
∵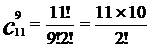 ,
,
又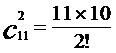 ,
,
∴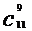 =
=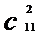 ;
;
∵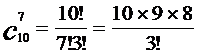
又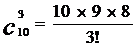
∴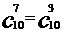 ;
;
∵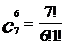
又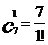
∴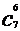 =
=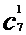 。
。
由不完全归纳可得:从n个不同的元素中取出m 个元素的组合数,等于从n个不同的元素中取出n-m个元素的组合数。即
定理1: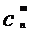 =
=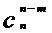 ,(n,m∈N,且m≤N)
,(n,m∈N,且m≤N)
(2)定理1的证明。要证明这个等式成立,即证明两个量相等。那么,证明两个量相等有声么方法呢?(指明学生回答)
方法一:“若两个数都等于第三个数,则这两个数相等 ”。
我们知道,
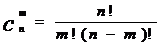 ,
,
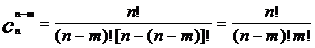
显然,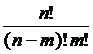 等于
等于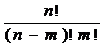 。于是可得下面的证明。
。于是可得下面的证明。
证明:∵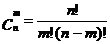 ,
,
又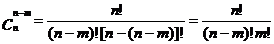 ,
,
∴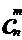 =
=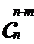 。
。
(3)性质1的另一种解释:从n个不同的元素中取出m个元素,并成一组,那么,剩下的n-m个元素也成一组;反之,从n个不同的元素中取出n-m个元素并组成一组,那么剩下的m个元素也成一组。所以,它们的组合是一一对应的,故有从n个不同的元素中取出m个的组合数是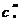 等于从 n个不同的元素中取出n-m个元素的组合数
等于从 n个不同的元素中取出n-m个元素的组合数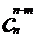 ,即
,即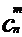 =
=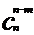 。
。
(4)当 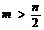 时,利用这个公式,可是
时,利用这个公式,可是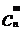 的计算简化。如:
的计算简化。如:
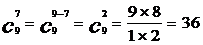 ,
,
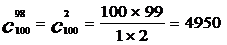 。
。
(5) 注意:当m=n时,公式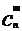 =
=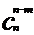 变形为
变形为
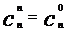 ,
,
又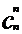 =1,所以规定:
=1,所以规定: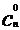 =1即 0!=1
=1即 0!=1
(6)在这样的一组组合数:
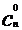 ,
,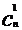 ,
,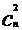 ……
……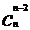 ,
,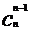 ,
,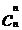
中,性质1还说明了:与两端等距离的两个组合数相等。如:
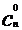 =
=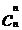 ,
,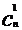 =
=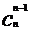 ,
,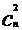 =
=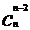 ,……。
,……。
2. 用计算的方法验证下列各式成立,并加以证明。
(1) (1)用计算的方法考察组合数:
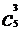 与
与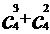 ,
, 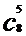 与
与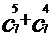
的关系,你能由此发现什么规律吗?(可指明学生回答,板书)
∵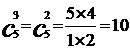
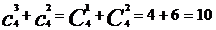
∴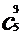 =
=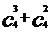
∵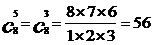
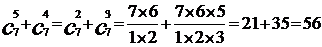
∴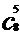 =
=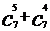
规律:若n、,m是自然数,m≤n,则
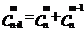 ,(或
,(或 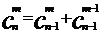 )
)
定理2 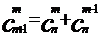 (n,m∈N,且m≤N)
(n,m∈N,且m≤N)
(2) 定理2的证明。要证明这个等式,只要根据组合数的公式变形即可。
证明:∵ 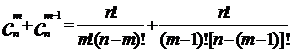
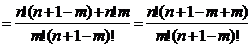
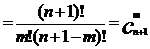
∴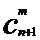
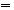
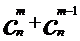
(3)对于定理2,还可以这样解释:从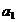 ,
, 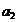 ,….,
,….,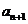 这n+1个不同的元素中取出m个元素的组合数
这n+1个不同的元素中取出m个元素的组合数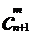 ,这些组合可以分成两类:一类含
,这些组合可以分成两类:一类含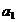 ,一类不含
,一类不含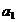 。含
。含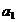 的组合是从
的组合是从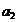 ,….,
,….,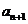 这n个不同的元素中取出m-1个元素的组合数为
这n个不同的元素中取出m-1个元素的组合数为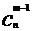 ,不含
,不含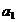 的组合是从
的组合是从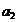 ,….,
,….,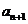 这n个不同的元素中取出m个元素的组合数为
这n个不同的元素中取出m个元素的组合数为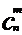 。再由加法原理,得:
。再由加法原理,得:
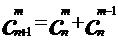 。
。
(3)定理2还说明了,把从n+1个不同的元素中取出m个元素的组合数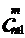 ,等于从n个不同的元素中取出m个元素的组合数
,等于从n个不同的元素中取出m个元素的组合数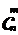 与从n个不同的元素中取出m-1个元素的组合数
与从n个不同的元素中取出m-1个元素的组合数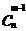 的和。这体现了组合数的可分解性,或组合数的可加性。
的和。这体现了组合数的可分解性,或组合数的可加性。
二、课堂练习:
1.
计算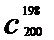 与
与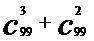 ;
;
2.
求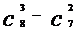 ;
;
3. 利用定理2证明:
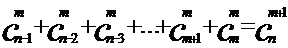
证明: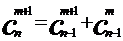
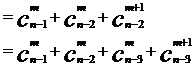
……
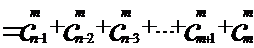
又证:将原式左边的各项写成:
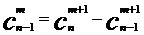 ,
, 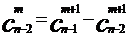 ,
, 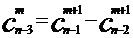 , ……
, ……
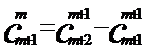 ,
,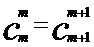 ,
,
将上述的等式两边相加,得:
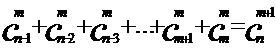
四、作业:认真阅读课文,重点掌握组合数的两个性质的证明和利用性质计算组合数的方法,并做下列练习:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com