(本小题满分12分)已知函数y＝|cosx＋sinx|.

(1)画出函数在x∈[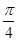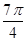－，]上的简图；

(2)写出函数的最小正周期和在[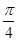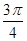－，]上的单调递增区间；试问：当x在R上取何值

时，函数有最大值？最大值是多少？

(3)若x是△ABC的一个内角，且y²＝1，试判断△ABC的形状．

(本小题满分12分)

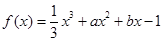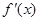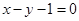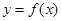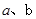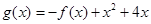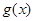 已知函数的导函数为偶函数，直线是的一条切线.(1).求的值 (2).若,求的极值.

(本小题满分12分)

已知某食品厂需要定期购买食品配料，该厂每天需要食品配料200千克，配料的价格为元/千克，每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用（若天购买一次，需要支付天的保管费）。其标准如下: 7天以内（含7天），无论重量多少，均按10元/天支付；超出7天以外的天数，根据实际剩余配料的重量，以每天0.03元/千克支付.

(1）当9天购买一次配料时，求该厂用于配料的保管费用是多少元？[

(2）设该厂天购买一次配料，求该厂在这天中用于配料的总费用（元）关于的函数关系式，并求该厂多少天购买一次配料才能使平均每天支付的费用最少?

.(本小题满分12分)

已知以函数f(x)＝mx³－x的图象上一点N(1，n)为切点的切线倾斜角为.

(1)求m、n的值；

(2)是否存在最小的正整数k，使得不等式f(x)≤k－1995，对于x∈[－1,3]恒成立？若存在，求出最小的正整数k，否则请说明理由．

(本小题满分12分)已知某食品厂需要定期购买食品配料，该厂每天需要食品配料200千克，配料的价格为元/千克，每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用，其标准如下: 7天以内（含7天），无论重量多少，均按10元/天支付；超出7天以外的天数，根据实际剩余配料的重量，以每天0.03元/千克支付.

（1）当9天购买一次配料时，求该厂用于配料的保管费用P是多少元？

（2）设该厂天购买一次配料，求该厂在这天中用于配料的总费用（元）关于的函数关系式，并求该厂多少天购买一次配料才能使平均每天支付的费用最少?