
题目列表(包括答案和解析)
 (2008•成都三模)如图1,在平行四边形ABCD中,AB=1,BD=
(2008•成都三模)如图1,在平行四边形ABCD中,AB=1,BD=| 2 |
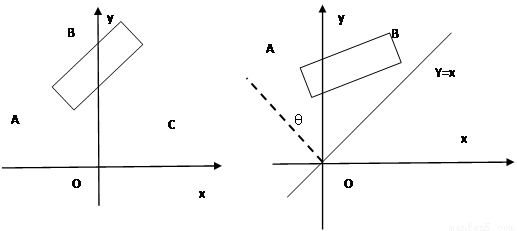
如图1,在平面直角坐标系中,边长为1的正方形OABC的顶点B在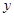 轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.
轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.
(1)当点A第一次落到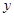 轴正半轴上时,求边BC在旋转过程中所扫过的面积;
轴正半轴上时,求边BC在旋转过程中所扫过的面积;
(2)若线段AB与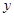 轴的交点为M(如图2),线段BC与直线
轴的交点为M(如图2),线段BC与直线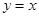 的交点为N.设
的交点为N.设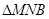 的周长为
的周长为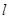 ,在正方形OABC旋转的过程中
,在正方形OABC旋转的过程中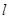 值是否有改变?并说明你的结论;
值是否有改变?并说明你的结论;
(3)设旋转角为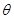 ,当
,当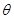 为何值时,
为何值时,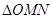 的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.
的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.

如图1,在平行四边形ABCD中,AB=1,BD= ,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.

(1)若F、G分别是AD、BC的中点,且AB∥平面EFG,求证:CD∥平面EFG;
(2)当图1中AE+EC最小时,求图2中二面角A-EC-B的大小.
如图1,在平面直角坐标系中,边长为1的正方形OABC的顶点B在 轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.
轴的正半轴上,O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.
(1)当点A第一次落到 轴正半轴上时,求边BC在旋转过程中所扫过的面积;
轴正半轴上时,求边BC在旋转过程中所扫过的面积;
(2)若线段AB与 轴的交点为M(如图2),线段BC与直线
轴的交点为M(如图2),线段BC与直线 的交点为N.设
的交点为N.设 的周长为
的周长为 ,在正方形OABC旋转的过程中
,在正方形OABC旋转的过程中 值是否有改变?并说明你的结论;
值是否有改变?并说明你的结论;
(3)设旋转角为 ,当
,当 为何值时,
为何值时, 的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.
的面积最小?求出这个最小值, 并求出此时△BMN的内切圆半径.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com