
题目列表(包括答案和解析)
 如图所示,在xoy平面内有一扇形金属框abc,其半径为r,ac边与y轴重合,bc边与x轴重合,且c为坐标原点,ac边与bc边的电阻不计,圆弧ab上单位长度的电阻为R.金属杆MN长度为L,放在金属框abc上,MN与ac边紧邻.磁感应强度为B的匀强磁场与框架平面垂直并充满平面.现对MN杆施加一个外力(图中未画出),使之以C点为轴顺时针匀速转动,角速度为ω.求:
如图所示,在xoy平面内有一扇形金属框abc,其半径为r,ac边与y轴重合,bc边与x轴重合,且c为坐标原点,ac边与bc边的电阻不计,圆弧ab上单位长度的电阻为R.金属杆MN长度为L,放在金属框abc上,MN与ac边紧邻.磁感应强度为B的匀强磁场与框架平面垂直并充满平面.现对MN杆施加一个外力(图中未画出),使之以C点为轴顺时针匀速转动,角速度为ω.求: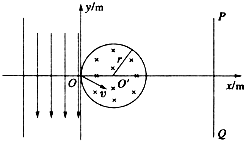 如图所示,在xOy平面内,y轴左侧有一个方向竖直向下,水平宽度为l=
如图所示,在xOy平面内,y轴左侧有一个方向竖直向下,水平宽度为l=| 3 |
 如图所示,在xOy平面内y>0的区域中存在垂直纸面向外的匀强磁场,磁感应强度大小为B0,在y<0的区域也存在垂直纸面向外的匀强磁场(图中未画出),一带正电的粒子从y轴上的P点垂直磁场入射,速度方向与y轴正向成45°.粒子第一次进入y<0的区域时速度方向与x轴正向成135°,再次在y>0的区域运动时轨迹恰与y轴相切.已知OP的距离为
如图所示,在xOy平面内y>0的区域中存在垂直纸面向外的匀强磁场,磁感应强度大小为B0,在y<0的区域也存在垂直纸面向外的匀强磁场(图中未画出),一带正电的粒子从y轴上的P点垂直磁场入射,速度方向与y轴正向成45°.粒子第一次进入y<0的区域时速度方向与x轴正向成135°,再次在y>0的区域运动时轨迹恰与y轴相切.已知OP的距离为| 2 |
 (2008?湖北模拟)如图所示,在xOy平面内,有场强E=12N/C,方向沿x轴正方向的匀强电场和磁感应强度大小为B=2T、方向垂直xOy平面指向纸里的匀强磁场.一个质量m=4×10-5kg,电量q=2.5×10-5C带正电的微粒,在xOy平面内做匀速直线运动,运动到原点O时,撤去磁场,经一段时间后,带电微粒运动到了x轴上的P点.求:
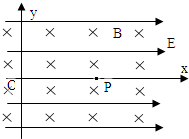
(2008?湖北模拟)如图所示,在xOy平面内,有场强E=12N/C,方向沿x轴正方向的匀强电场和磁感应强度大小为B=2T、方向垂直xOy平面指向纸里的匀强磁场.一个质量m=4×10-5kg,电量q=2.5×10-5C带正电的微粒,在xOy平面内做匀速直线运动,运动到原点O时,撤去磁场,经一段时间后,带电微粒运动到了x轴上的P点.求: 如图所示,在xOy平面内的第III象限中有沿-y方向的匀强电场,场强大小为E.只第I和第II象限有匀强磁场,磁场方向垂直于坐标平面向里,有一质量为m,电荷量为e的电子,从y轴的P点以初速度v0垂直于电场方向进入电场,P点坐标为(0,-
如图所示,在xOy平面内的第III象限中有沿-y方向的匀强电场,场强大小为E.只第I和第II象限有匀强磁场,磁场方向垂直于坐标平面向里,有一质量为m,电荷量为e的电子,从y轴的P点以初速度v0垂直于电场方向进入电场,P点坐标为(0,-m
| ||
| 2Ee |
| 4E |
| 3v0 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com