练习册

  • 练习册
  • 试题
    如图2中.套在竖直细杆上的轻环A由跨过定滑轮的不可伸长的轻绳与重物B相连.由于B的质量较大.故在释放B后.A将沿杆上升.当A环上升至与定滑轮的连线处于水平位置时.其上升速度v1≠0.若这时B的速度为v2.则( ) A.v2=v1 B.v2>v1 C.v2≠0 D.v2=0 [解析]选D.轻环上升过程其速度v1可分解为两个分速度v∥和v⊥.如图所示.其中v∥为沿绳方向的 速度.其大小等于重物B的速度v2,v⊥为绕定滑轮转动的线速度.关系式为v2=v1cosθ.θ为v1与v∥间的夹角.当A上升至与定滑轮的连线水平的位置时.θ=90°.cosθ=0.即此时v2=0.D正确. 【查看更多】

     

    题目列表(包括答案和解析)

    如图所示，V形细杆AOB能绕其对称轴OO′转动，OO′沿竖直方向，V形杆的两臂与转轴间的夹角均为α=45°．两质量均为m=0.1kg的小环，分别套在V形杆的两臂上，并用长为l=1.2m、能承受最大拉力Fmax=4.5N的轻质细线连结，环与臂间的最大静摩擦力等于两者间弹力的0.2倍．当杆以角速度ω转到时，细线始终处于水平状态，取g=10m/s2．
    （1）求杆转动角速度的最小值ωmin；
    （2）将杆的角速度从（1）问中求得的最小值开始缓慢增大，直到细线断裂，求细线断裂时转动的角速度ωm；
    （3）求角速度从ωmin增大到ωm的过程中杆对每个环所做的功．

    查看答案和解析>>

    如图所示，足够高的竖直墙壁M、N之间有一根水平光滑细杆，在杆上A点的左侧某位置处套有一细环，一 5量为m的小球用长为L的轻质细绳系在环上．N墙壁上的B点与小球等高，现让环与小球一起以V=
    		2gl
    的速度向右运动．环运动到A点被挡住而立即停止．已知杆上A点离N墙壁的水平距离为
    		2
    2
    L，细绳能承受的最大拉力为2.5mg．不计空气阻力，则下列说法中正确的是（　　）

    查看答案和解析>>

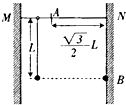    如图所示，足够高的竖直墙壁M、N之间有一根水平光滑细杆，在杆上A点的左侧某位置处套有一细环，一质量为m的小球用长为L的轻质细绳系在环上．N墙壁上的B点与小球等高，现让环与小球一起以V=
    		2gL
    的速度向右运动．环运动到A点被挡住而立即停止．已知杆上A点离N墙壁的水平距离为
    		3
    2
    L，细绳能承受的最大拉力为2.5mg．不计空气阻力，则下列说法中正确的是（　　）

    查看答案和解析>>

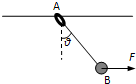    精英家教网如图所示，质量均为m的环A与球B用一轻质细绳相连，环A套在水平喜感上．现有一水平恒力F作用在球B上，使A环与B球一起向右匀速运动．已知细绳与竖直方向的夹角为θ．下列说法中正确的是（　　）

    查看答案和解析>>

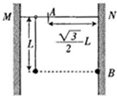    精英家教网如图所示，足够高的竖直墙壁M、N之间有一根水平光滑细杆，在杆上A点的左侧某位置处套有一细环，一质量为m的小球用长为L的轻质细绳系在环上．N墙壁上的B点与小球等高，现让环与小球一起以v=
    		2gL
    的速度向右运动．环运动到A点被挡住而立即停止．已知杆上A点离N墙壁的水平距离为
    		3
    2
    L，细绳能承受的最大拉力为2.5mg．不计空气阻力，则下列说法中正确的是（　　）
    A、细绳不会断裂，与N墙壁碰前小球做圆周运动
    B、小球与N墙壁碰撞时的速度为
    		2gL
    C、小球与N墙壁的碰撞点到B点的距离为
    L
    2
    D、小球与N墙壁的碰撞点到B点的距离为
    3L
    16

    查看答案和解析>>


    同步练习册答案