
题目列表(包括答案和解析)
第一问 车和物体收到的力都是摩擦力
f=μmg 车的加速度a1=f/M=μmg/M=1m/s^2
滑块的加速度a2=f/m=μmg/m=5m/s^2
第二问 S=2.7m
假设不能从车上滑出 那么滑块最后必定停留在车上 并且和车具有同样的末速度 设为v'
因为系统在水平方向上所受的合外力为零 所以满足动量守恒
Mv+mv0=(M+m)*v' → v'=v0*m/(M+m)=7.5*10/(10+50)=1.25m/s
然后我们看能量 如果系统的初动能减去末动能 小于摩擦力所能做的最大功(就是滑块滑到头 但没掉下来) 那么假设成立 反之 不成立 不能明白的话 我们看下面具体的解答
先求系统的末动能 Ek'=1/2(M+m)v'^2=1/2*(50+10)*1.25^2=46.875(J)
系统的初动能 Ek=1/2mv0^2=1/2*10*7.5^2=281.25(J)
摩擦力所能做的最大功 W=fs=μmgs=0.5*10*10*3=150(J)
Ek-Ek'>W 所以也就是说 系统的初动能被摩擦力消耗掉一部分后【克服摩擦力做功】 所剩下的动能 还是要大于他们最后一起以同样的速度运动时的动能 因此滑块最后不肯能停在车上
那么 我们就来求滑块落地时与平板车右端间的水平距离
因为滑块滑出小车后 在水平方向上和小车都是做匀速运动
所以他们之间的距离 就是他们的速度差乘以滑块落地所需的时间
那么 我们就需要算出滑块的末速度v'和小车的末速度v''
现在有两个未知数 那就必须有两个方程
第一个方程是能量方程 Ek-W=1/2mv'^2+1/2Mv''^2
第二个方程是动量方程 mv0=mv'+Mv''
联立这两个方程 解得 v''=0.5m/s 或 v''=2m/s(舍掉)
从而得到v'=5m/s
接下来算滑块落地要多长时间
由h=1/2gt^2 带入数据 得t=0.6s
所以最后的答案: S=(v'-v'')*t=4.5*0.6=2.7m
 ,AB是一条直径,今有一束平行光沿AB方向射向圆柱体,试求:
,AB是一条直径,今有一束平行光沿AB方向射向圆柱体,试求:

 (1)某同学设计了一个测量物体质量的装置,如图1所示,其中P是光滑水平轨道,A是质量为M的带夹子的已知质量金属块,Q是待测质量的物体(可以被A上的夹子固定).已知该装置的弹簧振子做简谐运动的周期为T=2π
(1)某同学设计了一个测量物体质量的装置,如图1所示,其中P是光滑水平轨道,A是质量为M的带夹子的已知质量金属块,Q是待测质量的物体(可以被A上的夹子固定).已知该装置的弹簧振子做简谐运动的周期为T=2π| m/k |
| ω(rad/s) | 0.5 | 1 | 2 | 3 | 4 |
| N | 5 | 20 | 80 | 180 | 320 |
| Ek(J) |
| 10 |
| π |
(1)(9分)某同学设计了一个测量物体质量的装置,如图所示,其中P是光滑水平轨道,A是质量为M的带夹子的已知质量金属块,Q是待测质量的物体(可以被A上的夹子固定)。已知该装置的弹簧振子做简谐运动的周期为![]() ,其中m是振子的质量,k是与弹簧的劲度系数有关的常数。
,其中m是振子的质量,k是与弹簧的劲度系数有关的常数。
① 简要写出测量方法及所需测量的物理量(用字母表示)
A.
B.
② 用所测物理量和已知物理量求解待测物体质量的计算式为m=
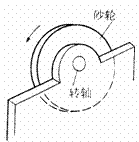
(2)(9分)物体因绕轴转动而具有的动能叫转动动能,转动动能的大小与物体转动的角速度有关。如图所示,为了研究某一砂轮的转动动能Ek与角速度ω和关系,可采用下述方法:先让砂轮由动力带动匀速旋转,测行其角速度ω,然后让砂轮脱离动力,由于克服转轴间摩擦力做功,砂轮最后停下。测出脱离动力到停止转动砂轮转过的转数n,测得几组不同的ω和n如下表所示:
ω(rad/s) | 0.5 | 1 | 2 | 3 | 4 |
N | 5 | 20 | 80 | 180 | 320 |
Ek(J) |
另外已测得砂轮转轴的直径为1cm,转轴间的摩擦力为![]() 。
。
① 试计算出每次脱离动力时砂轮的转动动能,并填入上表中
② 试由上述数据推导出该砂轮转动动能Ek与角速度ω的关系式Ek=
③ 若脱离动力后砂轮角速度为2.5rad/s,则它转过45转后角速度为 rad/s
![]()

 B.
B.
 D.
D.
 和M固定在轻质弹簧的两端,静止于光滑的水平面上.一质量为M/4的木块A以速度v水平向右与木块B对心碰撞,并粘在一起运动,求弹簧的最大弹性势能Em.
和M固定在轻质弹簧的两端,静止于光滑的水平面上.一质量为M/4的木块A以速度v水平向右与木块B对心碰撞,并粘在一起运动,求弹簧的最大弹性势能Em.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com