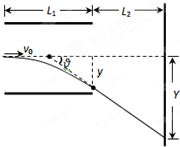如图，平行板间电压为U，板间距离为d，板长为L₁．一带电粒子质量为m，电荷量为q，以初速度v₀垂直于场强方向射入电场中，离开电场后沿直线打在荧光屏上．荧光屏到平行板右端的距离为L₂．不计粒子重力．求
（1）粒子在电场中运动的时间t₁；
（2）板间场强E和粒子在电场中运动的加速a；
（3）粒子在电场中的偏转分位移y₁；
（4）粒子离开电场后经多长时间t₂打到荧光屏上？

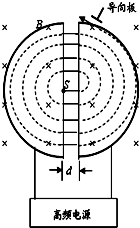如图为回旋加速器示意图，其中置于高真空中的金属D形盒的半径为R，两盒间距为d（d＜＜R），在左侧D形盒圆心处放有粒子源S，匀强磁场的磁感应强度为B，方向如图所示．质子质量为m，电荷量为q．设质子从粒子源S进入加速电场时的初速度不计，加速质子时的电压恒为U，质子在电场中运动时，不考虑磁场的影响．求：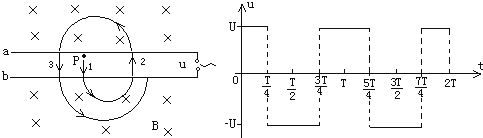
（1）此加速器所需的高频电源频率f；
（2）质子能达到的最大速度；
（3）质子在电场中运动的时间和在D形盒中回旋的时间，并说明质子在电场中加速的时间可忽略不计．

在D型盒回旋加速度器中，高频交变电压（假设为右图所示的方形波）加在a板和b板间，带电粒子在a、b间的电场中加速，电压大小为U=800V，在匀强磁场中做匀速圆周运动，磁感应强度大小B=0.628T，a板与b板间的距离d=0.1mm，被加速的粒子为质子，质子的质量约为m=1.6×10^-27kg，电荷量为q=1.6×10^-19C．t=0时刻，静止的质子从靠近a板的P点开始第1次加速，t=T/2时刻恰好第2次开始加速，t=T时刻恰好第3次开始加速，…，每隔半个周期加速一次．（每一次加速的时间与周期相比可以忽略，不考虑相对论中因速度大而引起质量变化的因素）

（1）求交变电压的周期T．
（2）求第900次加速结束时，质子的速度多大？
（3）虽然每一次的加速时间可以忽略，但随着加速次数的增多，在电场中运动的时间累积起来就不能忽略了．求第n次完整的加速过程结束时质子在ab间电场中加速运动的总时间t（用相关物理量的字母符号如U、d…表示，不需代入数值）

如图所示，真空中有两个等量异种点电荷A和B，一带负电的试探电荷仅受电场力作用，在电场中运动的部分轨迹如图中实线所示．M、N是轨迹上的两点，MN连线与AB连线垂直，O为垂足，且AO＞OB．设M、N两点的场强大小分别为E_M、E_N，电势分别为φ_M、φ_N．下列判断中正确的是（　　）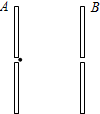

如图所示，A、B为真空中相距为d的一对平行金属板，两板间的电压为U，一带电粒子从A板的小孔进入电场，粒子的初速度可视为零，经电场加速后从B板小孔射出．已知带电粒子的质量为m，所带电荷量为q．带电粒子所受重力不计．求：
（1）带电粒子从B板射出时的速度大小；
（2）带电粒子在电场中运动的时间．