
题目列表(包括答案和解析)
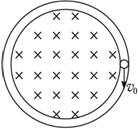
图18-3-8
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
如图18-3-8所示,半径为r且水平放置的光滑绝缘的环形管道内,有一个电荷量为e,质量为m的电子.此装置放在匀强磁场中,其磁感应强度随时间变化的关系式为B=B0+kt(k>0).根据麦克斯韦电磁场理论,均匀变化的磁场将产生稳定的电场,该感应电场对电子将有沿圆环切线方向的作用力,使其得到加速.设t=0时刻电子的初速度大小为v0,方向顺时针,从此开始运动一周后的磁感应强度为B1,则此时电子的速度大小为( )
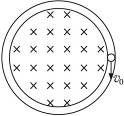
图18-3-8
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

A. | B. | C. | D. |

(1)小球的最小动能是多少?
(2)若小球在动能最小位置时突然撤去轨道,并保持其他量都不变,则小球经0.4 s时间后,其动能与在A点时的动能相等,则小球的质量为多少?
(3)若θ=60°,取圆轨道的最低点重力势能为零,并利用(2)中所求小球的质量,在轨道未撤去的情况下,试求小球的最大机械能是多少。
如图所示,半径R=0.8 m的四分之一光滑圆弧轨道位于竖直平面内,与长CD=2.0 m的绝缘水平面平滑连接.水平面右侧空间存在互相垂直的匀强电场和匀强磁场,电场强度E=40 N/C,方向竖直向上,磁场的磁感应强度B=1.0 T,方向垂直纸面向外.两个质量均为m=2.0×10-6 kg的小球a和b,a球不带电,b球带q=1.0×10-6 C的正电,并静止于水平面右边缘处.将a球从圆弧轨道顶端由静止释放,运动到D点与b球发生正碰,碰撞时间极短,碰后两球粘合在一起飞入复合场中,最后落在地面上的P点.已知小球a在水平面上运动时所受的摩擦阻力f=0.1 mg,PN=![]() ,取g=10 m/s2.a、b均可作为质点.求:
,取g=10 m/s2.a、b均可作为质点.求:

(1)小球a与b相碰后瞬间速度的大小v;
(2)水平面离地面的高度h;
(3)从小球a开始释放到落地前瞬间的整个运动过程中,ab系统损失的机械能ΔE.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com