解：作BE⊥l于点E，DF⊥l于点F．                   ……2分

∵∠α+∠DAF=180°-∠BAD=180°-90°=90°，∠ADF+∠DAF=90°，

∴∠ADF=∠α=36°．根据题意，得BE=24mm, DF=48mm． ……4分

在Rt△ABE中，sinα=BE/AB，∴AB=BE/sin36°=40(mm).……6分

在Rt△ADF中，cos∠ADF=DF/AD，∴AD=DF/COS36°=60(mm）．8分

∴矩形ABCD的周长=2(40+60)=200(mm)．             ……10分

如图，梯形ABCD中，AD∥BC，AC与BD相交于O点，过点B作BE∥CD交CA的延长线于点E．求证：OC²=OA•OE．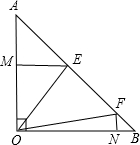

如图，已知等腰Rt△AOB，其中∠AOB=90°，OA=OB=2，E、F为斜边AB上的两个动点（E比F更靠近A），满足∠EOF=45°，
（1）求证：△AOF∽△BEO；
（2）求AF•BE的值；
（3）作EM⊥OA于M，FN⊥OB于N，求OM•ON的值；
（4）求线段EF长的最小值．（提示：必要时可以参考以下公式：当x＞0，y＞0时，x+y=(

x

-

y

)2+2

xy

或x+

1

x

=(

x

-

1

x

)2+2）