
题目列表(包括答案和解析)
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 29 |
| 1 |
| 29 |
 某校为开展“阳光体育”运动,丰富学生课间自由活动内容,随机选取了本校100名学生进行调查,调查的内容是:你最喜欢的自由活动项目是什么?,将收集到的数据整理,给出了如图10所示的统计图.
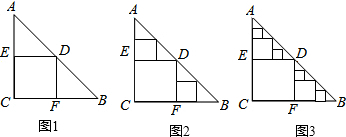
某校为开展“阳光体育”运动,丰富学生课间自由活动内容,随机选取了本校100名学生进行调查,调查的内容是:你最喜欢的自由活动项目是什么?,将收集到的数据整理,给出了如图10所示的统计图.△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲.乙两种剪法,哪种剪法所得的正方形面积大?请说明理由。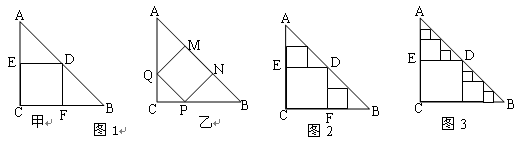
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为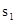 ;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为
;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为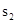 (如图2),则
(如图2),则 ;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为
;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为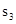 ,继续操作下去……,则第10次剪取时,
,继续操作下去……,则第10次剪取时, ;
;
(3)求第10次剪取后,余下的所有小三角形的面积之和。
△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,(1)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图1),比较甲.乙两种剪法,哪种剪法所得的正方形面积大?请说明理由。
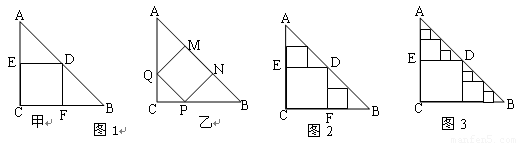
(2)图1中甲种剪法称为第1次剪取,记所得正方形面积为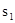 ;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为
;按照甲种剪法,在余下的△ADE和△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为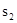 (如图2),则
(如图2),则 ;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为
;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第3次剪取,并记这四个正方形面积和为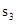 ,继续操作下去……,则第10次剪取时,
,继续操作下去……,则第10次剪取时, ;
;
(3)求第10次剪取后,余下的所有小三角形的面积之和。
某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图10所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
求出样本容量,并补全直方图;
该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com