
题目列表(包括答案和解析)
已知,O为正方形ABCD对角线上一点,以O为圆心,OA的长为半径的⊙O与BC相切于M,与AB、AD分别相交于E、F.

(1)求证:CD与⊙O相切.
(2)若正方形ABCD的边长为1,求⊙O的半径.
(3)对于以点M、E、A、F以及CD与O⊙的切点为顶点的五边形的五条边,从相等的关系考虑,你可以得出什么结论?请你给出证明
如图所示,已知△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足为E、F.
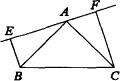
(1)证明过A的直线与斜边BC不相交时,有EF=BE+CF.
(2)如图所示,过A的直线与斜边BC相交时,其他条件不变,你能得出什么结论,请你给出证明.
阅读下列例题的解题过程,给出问题的解答.

已知a2-4a-2=0,求a3-3a 2-6a+30的值.
阅读下列例题的解题过程,给出问题的解答.
已知a2-4a-2=0,求a3-3a 2-6a+30的值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com