
题目列表(包括答案和解析)
 (2013•香坊区二模)如图,在平面直角坐标系中,O为坐标原点,直线y=x+4与x轴交于点A,与y轴交于点B,点C在x轴负半轴上,S△ABC=28.点P从C出发沿CA向终点A运动,设P点坐标为(t,0).
(2013•香坊区二模)如图,在平面直角坐标系中,O为坐标原点,直线y=x+4与x轴交于点A,与y轴交于点B,点C在x轴负半轴上,S△ABC=28.点P从C出发沿CA向终点A运动,设P点坐标为(t,0).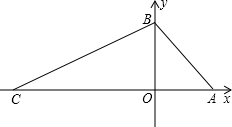 如图,在平面直角坐标系中,O为坐标原点,直线y=x+4与x轴交于点A,与y轴交于点B,点C在x轴负半轴上,S△ABC=28.点P从C出发沿CA向终点A运动,设P点坐标为(t,0).
如图,在平面直角坐标系中,O为坐标原点,直线y=x+4与x轴交于点A,与y轴交于点B,点C在x轴负半轴上,S△ABC=28.点P从C出发沿CA向终点A运动,设P点坐标为(t,0).(2006黑龙江课改,28)(10分)如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是方程 的两个根,点C是线段AB的中点,点D在线段OC上,OD=2CD.
的两个根,点C是线段AB的中点,点D在线段OC上,OD=2CD.
(1)求点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

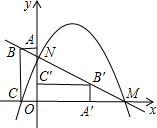 如图,在平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0),将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.设直线BB′与x轴交于点M、与y轴交于点N,抛物线y=ax2+2x+c的图象经过点C、M、N.解答下列问题:
如图,在平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0),将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.设直线BB′与x轴交于点M、与y轴交于点N,抛物线y=ax2+2x+c的图象经过点C、M、N.解答下列问题: 如图,在平面直角坐标系中,已知点A(3,2)和点B(5,0),试求sin∠AOB和tan∠ABO的值.
如图,在平面直角坐标系中,已知点A(3,2)和点B(5,0),试求sin∠AOB和tan∠ABO的值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com