
题目列表(包括答案和解析)
 阅读理解
阅读理解
|
|

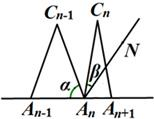
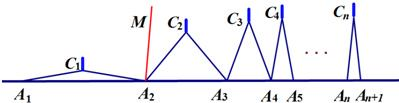
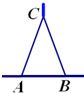 小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-
小知识:如图,我们称两臂长度相等(即CA=CB)的圆规为等臂圆规.当等臂圆规的两脚摆放在一条直线上时,若张角∠ACB=x°,则底角∠CAB=∠CBA=(90-| x | 2 |
 如图,是一个长方形分成大小不等的6个小正方形,已知中间的最小的正方形的边长为1厘米,求这个长方形的面积
如图,是一个长方形分成大小不等的6个小正方形,已知中间的最小的正方形的边长为1厘米,求这个长方形的面积湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com