
题目列表(包括答案和解析)
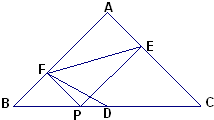 22、如图,在等腰Rt△ABC中,∠A=90°,D为斜边的中点.在DB上任取一点P,过P作两腰的垂线段PF、PE.连接EF.求证:EF2=2DF2.
22、如图,在等腰Rt△ABC中,∠A=90°,D为斜边的中点.在DB上任取一点P,过P作两腰的垂线段PF、PE.连接EF.求证:EF2=2DF2.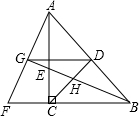
| 2 |
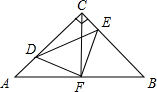 如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.
如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF. 如图,在等腰Rt△ABC中,∠ACB=90°,F是AB边上的中点,点D,E分别在AC,BC边上运动,且始终保持AD=CE,连接DE,DF,EF.探究:
如图,在等腰Rt△ABC中,∠ACB=90°,F是AB边上的中点,点D,E分别在AC,BC边上运动,且始终保持AD=CE,连接DE,DF,EF.探究: (2013•凤阳县模拟)如图,在等腰Rt△ABC中斜边BC=9,从中裁剪内接正方形DEFG,其中DE在斜边BC上,点F、G分别在直角边AC、AB上,按照同样的方式在余下的三角形中继续裁剪,如此操作下去,共可裁剪出边长大于1的正方形个数为( )
(2013•凤阳县模拟)如图,在等腰Rt△ABC中斜边BC=9,从中裁剪内接正方形DEFG,其中DE在斜边BC上,点F、G分别在直角边AC、AB上,按照同样的方式在余下的三角形中继续裁剪,如此操作下去,共可裁剪出边长大于1的正方形个数为( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com