
题目列表(包括答案和解析)
解:(1)A(-1,0),B(3,0),C(0,3).·················· 2分
抛物线的对称轴是:x=1.······················· 3分
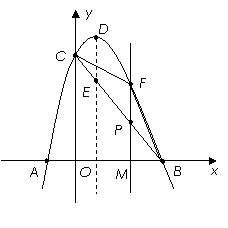 (2)①设直线BC的函数关系式为:y=kx+b.
(2)①设直线BC的函数关系式为:y=kx+b.
把B(3,0),C(0,3)分别代入得:
![]() 解得:k= -1,b=3.
解得:k= -1,b=3.
所以直线BC的函数关系式为:![]() .
.
当x=1时,y= -1+3=2,∴E(1,2).
当![]() 时,
时,![]() ,
,
∴P(m,![]() m+3).·························· 4分
m+3).·························· 4分
在![]() 中,当
中,当![]() 时,
时,![]()
∴![]()
当![]() 时,
时,![]() ∴
∴![]() ········· 5分
········· 5分
∴线段DE=4-2=2,线段![]() ···· 6分
···· 6分
∵![]()
∴当![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
由![]() 解得:
解得:![]() (不合题意,舍去).
(不合题意,舍去).
因此,当![]() 时,四边形
时,四边形![]() 为平行四边形.··········· 7分
为平行四边形.··········· 7分
②设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,由
,由![]() 可得:
可得:![]()
∵![]() ························ 8分
························ 8分
即![]() .
.
![]()
![]() ·········· 9分
·········· 9分
| 1 | 2 |
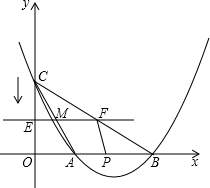 的图形是平行四边形、等腰梯形和等腰直角三角形?
的图形是平行四边形、等腰梯形和等腰直角三角形?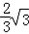 x+2与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点.
x+2与x轴交于C.A两点,与y轴交于点B,OB=4.点O关于直线AB的对称点为D,E为线段AB的中点. 的图象过点D,求k值;
的图象过点D,求k值; 个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值;若不存在,请说明理由.
.如同,抛物线![]()
![]() 与
与![]() 轴交于C、A两点,与y轴交于点B,OB=4点O关于直线AB的对称点为D,E为线段AB的中点.
轴交于C、A两点,与y轴交于点B,OB=4点O关于直线AB的对称点为D,E为线段AB的中点.
(1) 分别求出点A、点B的坐标
(2) 求直线AB的解析式
(3) 若反比例函数![]() 的图像过点D,求
的图像过点D,求![]() 值.
值.
(4)两动点P、Q同时从点A出发,分别沿AB、AO方向向B、O移动,点P每秒移动1个单位,点Q
每秒移动![]() 个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值,若不存在,请说明理由.
个单位,设△POQ的面积为S,移动时间为t,问:S是否存在最大值?若存在,求出这个最大值,并求出此时的t值,若不存在,请说明理由.
 |
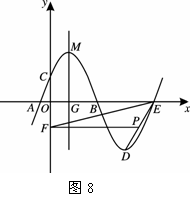
如图8,抛物线![]() :
:![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() ,将抛物线
,将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,得到新的抛物线
,得到新的抛物线![]() ,它的顶点为
,它的顶点为![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)设抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() ,点
,点![]() 是线段
是线段![]() 上一个动点(
上一个动点(![]() 不与
不与![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .如果
.如果![]() 点的坐标为
点的坐标为![]() ,
,![]() 的面积为S,求S与
的面积为S,求S与![]() 的函数关系式,写出自变量
的函数关系式,写出自变量![]() 的取值范围,并求出S的最大值;
的取值范围,并求出S的最大值;
(3)设抛物![]() 线
线![]() 的对称轴与
的对称轴与![]() 轴的交点为
轴的交点为![]() ,以
,以![]() 为圆心,
为圆心,![]() 两点间的距离为直径作⊙
两点间的距离为直径作⊙![]() ,试判断直线
,试判断直线![]() 与⊙
与⊙![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com