冰冰和亮亮想测量设在某建筑物顶上的广告牌离地面的高度。如图9，他俩分别站在这座建筑物的两侧，并所站的位置与该建筑物在同一条直线上，相距110米，他们分别测得仰角分别是39°和28°，已知测角仪的高度是1米，试求广告牌离地面的高度（精确到1米）

如图，直线l₁分别交x轴、y轴于A、B两点，且AO=8，BO=8

3

，与直线y=

3

x交于点C．平行于y轴的直线L₂从原点O出发，以每秒1个单位长度的速度沿x轴向右平移，到C点时停止；l₂分别交线段BC、OC、x轴于点D、E、P，以DE为边向左侧作等边△DEF，设直线l₂的运动时间为t（秒）．
（1）直接写出直线l₁的解析式；
（2）以D、E、O、F为顶点的多边形能否为梯形，若能，求出此时t的值；若不能，请说明理由；
（3）设△DEF与△BCO重叠部分的面积为S（平方单位），试探究：S与t的函数关系式．

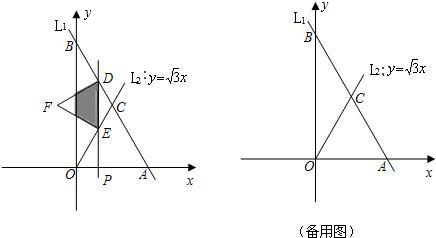
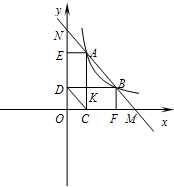如图，直线MN分别与x轴、y轴交于点M，N，与反比例函数y=

k

x

（x＞0）的图象相交于点A，B．过点A分别作AC⊥x轴，AE⊥y轴，垂足分别为C，E；过点B分别作BF⊥x轴，BD⊥y轴，垂足分别为F，D，AC与BD交于点K，连接CD．
（1）比较大小：S_{四边形AEOC}S_{四边形ODBF}；（填“＞，=，＜”）
（2）求证：

AK

BK

=

CK

DK

；
（3）试判断AN与BM有怎样的数量关系，并说明理由．