练习册

  • 练习册
  • 试题
    本题共有2个小题.第1小题满分6分.第2小题满分8分. 已知正三棱锥的体积为.侧面与底面所成的二面角的大小为.(1)证明:, (2)求底面中心到侧面的距离. [证明](1)取边的中点.连接.. 则..故平面. -- 4分 ∴ . -- 6分 [解]可知平面平面.则是侧面与底面所成二面角的平面角. 过点作为垂足.则就是点到侧面的距离. -- 9分 设为.由题意可知点在上. ∴ .. , -- 11分 ∴ . ∵ .∴ . 即底面中心到侧面的距离为3. -- 14分 【查看更多】

     

    题目列表(包括答案和解析)

    本题共有2个小题，第1小题满分6分，第2小题满分10分．
    已知a为实数，f(x)=a-
    22x+1
    (x∈R)    ．
    （1）求证：对于任意实数a，y=f（x）在（-∞，+∞）上是增函数；
    （2）当f（x）是奇函数时，若方程f-1（x）=log2（x+t）总有实数根，求实数t的取值范围．

    查看答案和解析>>

    （2005•上海模拟）本题共有2个小题，第1小题满分8分，第2小题满分6分
    过直角坐标平面xOy中的抛物线y2?2px （p＞0）的焦点F作一条倾斜角为
    π4
    的直线与抛物线相交于A、B两点．
    （1）用p表示A、B之间的距离并写出以AB为直径的圆C方程；
    （2）若圆C于y轴交于M、N两点，写出M、N的坐标，证明∠MFN的大小是与p无关的定值，并求出这个值．

    查看答案和解析>>

    （本题满分14分）本题共有2个小题，第1小题满分8分，第2小题满分6分.

    为保护环境，某单位采用新工艺，把二氧化碳转化为一种可利用的化工产品。已知该单位每月的处理量最多不超过300吨，月处理成本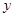（元）与月处理量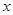（吨）之间的函数关系式可近似的表示为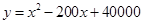：，且每处理一吨二氧化碳得到可利用的化工产品价值为300元。

    （1）该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？

    （2）要保证该单位每月不亏损，则每月处理量应控制在什么范围？

     

    查看答案和解析>>

    （本题满分14分）本题共有2个小题，第1小题满分7分，第2小题满分7分．

    已知△的周长为，且．

    　　（1）求边长的值；

    　　（2）若（结果用反三角函数值表示）．

    查看答案和解析>>

    （本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.
    如图，某公司要在两地连线上的定点处建造广告牌，其中为顶端，长35米，长80米，设在同一水平面上，从和看的仰角分别为.

    （1）设计中是铅垂方向，若要求，问的长至多为多少（结果精确到0.01米）？
    （2）施工完成后.与铅垂方向有偏差，现在实测得求的长（结果精确到0.01米）？

    查看答案和解析>>


    同步练习册答案