(1)当且仅当m为何值时，经过两点A(－m,6)，B(1,3m)的直线的斜率为12?

(2)当且仅当m为何值时，经过两点A(m,2)，B(－m,2m－1)的直线的倾斜角是60°？

[分析]　利用斜率公式列方程求解．

如下图所示，一个矩形花园里需要铺设两条笔直的小路，已知矩形花园的长AD＝5 m，宽AB＝3 m，其中一条小路定为AC，另一条小路过点D，问是否在BC上存在一点M，使得两条小路AC与DM相互垂直？若存在，则求出小路DM的长．

[分析]　建立适当的坐标系，转几何问题为代数运算．

如图所示，4×3的矩形(每个小方格都是单位正方形)，在起点和终点都在小方格的顶点处的向量中，试问：

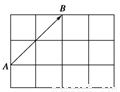
(1)与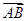相等的向量共有几个；

(2)与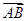平行且模为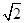的向量共有几个？

(3)与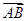方向相同且模为3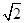的向量共有几个？

[分析]　非零向量平行(共线)包括两种情况：一种是方向相同，另一种是方向相反．

如图所示的几何体是一棱长为4cm的正方体，若在其中一个面的中心位置上，挖一个直径为2cm、深为1cm的圆柱形的洞，求挖洞后几何体的表面积是多少？(π取3.14)

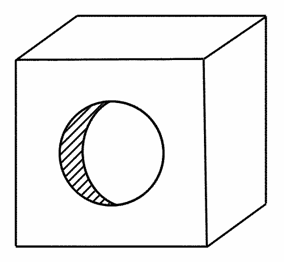
[分析]　因为正方体的棱长为4cm，而洞深只有1cm，所以正方体没有被打透．这样一来打洞后所得几何体的表面积等于原来正方体的表面积，再加上圆柱的侧面积，这个圆柱的高为1cm，底面圆的半径为1cm.