
题目列表(包括答案和解析)
把![]() 的反函数
的反函数![]() 图象向右平移2个单位就得到曲线C,函数
图象向右平移2个单位就得到曲线C,函数![]() 的图象与曲线C关于
的图象与曲线C关于![]() 成轴对称,那么
成轴对称,那么![]() 等于
等于
[ ]
| ωx |
| 2 |
| ωx |
| 2 |
| ωx |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 8 |
| π |
| 2 |
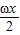 )cos
)cos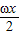 +cos2
+cos2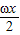
 ,(ω>0)
,(ω>0) 倍(纵坐标不变),再把所得的函数图象向右平移
倍(纵坐标不变),再把所得的函数图象向右平移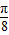 个单位得到函数y=g(x)的图象,求y=g(x)解析式,并求其对称中心.
个单位得到函数y=g(x)的图象,求y=g(x)解析式,并求其对称中心.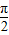 ,π]上是减函数,求ω的取值范围.
,π]上是减函数,求ω的取值范围.| ωx |
| 2 |
| ωx |
| 2 |
| ωx |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 8 |
| π |
| 2 |
 (2007•金山区一模)(1)已知平面上两定点A(-2,0)、B(2,0),且动点M的坐标满足
(2007•金山区一模)(1)已知平面上两定点A(-2,0)、B(2,0),且动点M的坐标满足| MA |
| MB |
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| b |
| x2 |
| a2 |
| y2 |
| b2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com