已知，函数（其中为自然对数的底数）．

  （Ⅰ）求函数在区间上的最小值；

  （Ⅱ）设数列的通项，是前项和，证明：．

【解析】本试题主要考查导数在研究函数中的运用，求解函数给定区间的最值问题，以及能结合数列的相关知识，表示数列的前n项和，同时能构造函数证明不等式的数学思想。是一道很有挑战性的试题。

设函数在处取得极值，且曲线在点处的切线垂直于直线.

(Ⅰ) 求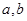的值；

（Ⅱ）求曲线和直线所围成的封闭图形的面积；

（Ⅲ）设函数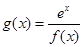，若方程有三个不相等的实根，求的取值范围.

【解析】本试题主要考查了导数的运用。利用导数求解曲边梯形的面积，以及求解函数与方程的根的问题的综合运用。