
题目列表(包括答案和解析)
A.变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫相关关系
B.在平面直角坐标系中,可以用散点图发现变量之间的变化规律
C.线性回归方程代表了观测值x、y之间的关系
D.任何一组观测值都能得到具有代表意义的回归直线方程
本题有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2个小题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4—2:矩阵与变换
在平面直角坐标系 中,把矩阵
中,把矩阵 确定的压缩变换
确定的压缩变换 与矩阵
与矩阵 确定的旋转变换
确定的旋转变换 进行复合,得到复合变换
进行复合,得到复合变换 .
.
(Ⅰ)求复合变换 的坐标变换公式;
的坐标变换公式;
(Ⅱ)求圆
 在复合变换
在复合变换 的作用下所得曲线
的作用下所得曲线 的方程.
的方程.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (
(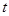 为参数),
为参数), 、
、 分别为直线
分别为直线 与
与 轴、
轴、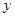 轴的交点,线段
轴的交点,线段 的中点为
的中点为 .
.
(Ⅰ)求直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,求点
轴的正半轴为极轴建立极坐标系,求点 的极坐标和直线
的极坐标和直线 的极坐标方程.
的极坐标方程.
(3)(本小题满分7分)选修4—5:不等式选讲
已知不等式 的解集与关于
的解集与关于 的不等式
的不等式 的解集相等.
的解集相等.
(Ⅰ)求实数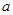 ,
, 的值;
的值;
(Ⅱ)求函数 的最大值,以及取得最大值时
的最大值,以及取得最大值时 的值.
的值.
本题有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2个小题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4—2:矩阵与变换
在平面直角坐标系 中,把矩阵
中,把矩阵 确定的压缩变换
确定的压缩变换 与矩阵
与矩阵 确定的旋转变换
确定的旋转变换 进行复合,得到复合变换
进行复合,得到复合变换 .
.
(Ⅰ)求复合变换 的坐标变换公式;
的坐标变换公式;
(Ⅱ)求圆
 在复合变换
在复合变换 的作用下所得曲线
的作用下所得曲线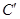 的方程.
的方程.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),
为参数), 、
、 分别为直线
分别为直线 与
与 轴、
轴、 轴的交点,线段
轴的交点,线段 的中点为
的中点为 .
.
(Ⅰ)求直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,求点
轴的正半轴为极轴建立极坐标系,求点 的极坐标和直线
的极坐标和直线 的极坐标方程.
的极坐标方程.
(3)(本小题满分7分)选修4—5:不等式选讲
已知不等式 的解集与关于
的解集与关于 的不等式
的不等式 的解集相等.
的解集相等.
(Ⅰ)求实数 ,
, 的值;
的值;
(Ⅱ)求函数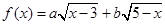 的最大值,以及取得最大值时
的最大值,以及取得最大值时 的值.
的值.
| n |
| n |
| n |
| n |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com