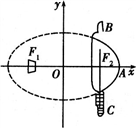
如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN，要求B在AM上，D在AN上，且对角线MN过C点，|AB|＝3米，|AD|＝2米，

（I）要使矩形AMPN的面积大于32平方米，则AN的长应在什么范围内？

（II）当AN的长度是多少时，矩形AMPN的面积最小？并求出最小面积．

（Ⅲ）若AN的长度不少于6米，则当AN的长度是多少时，矩形AMPN的面积最小？并求出最小面积．

【解析】本题主要考查函数的应用，导数及均值不等式的应用等，考查学生分析问题和解决问题的能力   第一问要利用相似比得到结论。

（I）由S_AMPN > 32 得 > 32 ，

∵x >2，∴，即（3x－8）（x－8）> 0

∴2<X<8/3，即AN长的取值范围是(2,8/3)或(8，+)

第二问，  

当且仅当

(3)令

∴当x > 4，y′> 0，即函数y＝在（4，＋∞）上单调递增，∴函数y＝在[6，＋∞]上也单调递增．                

∴当x＝6时y＝取得最小值，即S_AMPN取得最小值27（平方米）．

建造一个容积为18 m³，深为2 m的长方体无盖水池，如果池底和池壁每平方米的造价分别为200元和150元，那么池的最低造价为__________.

本题考查均值不等式的应用.

（本小题考查基本不等式的应用）已知，

则的最小值是  

A.2   B.    C.4   D.5

A．不等式的解集为      
B.如图，已知的两条直角边的长分别为3cm,4cm，以为直径的圆与交于点，则      ．

C.已知圆的参数方程为（为参数）以原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为，则直线与圆的交点的直角坐标系为_______