
题目列表(包括答案和解析)
设点 为平面直角坐标系
为平面直角坐标系 中的一个动点(其中O为坐标原点),点P到定点
中的一个动点(其中O为坐标原点),点P到定点 的距离比点P到
的距离比点P到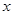 轴的距离大
轴的距离大 。
。
(1)求点P的轨迹方程。
(2)若直线 与点P的轨迹相交于A、B两点,且
与点P的轨迹相交于A、B两点,且 ,求
,求 的值。
的值。
(3)设点P的轨迹是曲线C,点 是曲线C上的一点,求以Q为切点的曲线C 的切线方程。
是曲线C上的一点,求以Q为切点的曲线C 的切线方程。
【解析】本试题主要考查了轨迹方程的求解,利用直接法设点表示轨迹方程,并能利用所求的轨迹进行直线与圆锥曲线位置关系的运用。以及导数的几何意义的运用的综合试题。
已知抛物线![]() ,过M(a,0)且斜率为1的直线
,过M(a,0)且斜率为1的直线![]() 与抛物线交于不同的两点A、B,
与抛物线交于不同的两点A、B,![]() 。
。
(1)求a的取值范围;
(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值。
分析:这是一道直线与圆锥曲线位置关系的问题,对于(1),可以设法得到关于a的不等式,通过解不等式求出a的范围,即“求范围,找不等式”。或者将a表示为另一个变量的函数,利用求函数的值域求出a的范围。对于(2)首先要把△NAB的面积表示为一个变量的函数,然后再求它的最大值。
设点 为平面直角坐标系
为平面直角坐标系 中的一个动点(其中O为坐标原点),点P到定点
中的一个动点(其中O为坐标原点),点P到定点 的距离比点P到
的距离比点P到 轴的距离大
轴的距离大 。
。
(1)求点P的轨迹方程。
(2)若直线 与点P的轨迹相交于A、B两点,且
与点P的轨迹相交于A、B两点,且 ,求
,求 的值。
的值。
(3)设点P的轨迹是曲线C,点 是曲线C上的一点,求以Q为切点的曲线C 的切线方程。
是曲线C上的一点,求以Q为切点的曲线C 的切线方程。
【解析】本试题主要考查了轨迹方程的求解,利用直接法设点表示轨迹方程,并能利用所求的轨迹进行直线与圆锥曲线位置关系的运用。以及导数的几何意义的运用的综合试题。
本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4-4:坐标系与参数方程
以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴。已知点
轴的正半轴为极轴。已知点 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点 的极坐标为
的极坐标为 若直线
若直线 过点
过点 ,且倾斜角为
,且倾斜角为 ,圆
,圆 以
以 为圆心、
为圆心、 为半径。
为半径。
(I)求直线 的参数方程和圆
的参数方程和圆 的极坐标方程;
的极坐标方程;
(II)试判定直线 和圆
和圆 的位置关系.
的位置关系.
(2)(本小题满分7分)选修4-4:矩阵与变换
把曲线 先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于
先进行横坐标缩为原来的一半,纵坐标保持不变的伸缩变换,再做关于 轴的反射变换变为曲线
轴的反射变换变为曲线 ,求曲线
,求曲线 的方程.
的方程.
(3)(本小题满分7分)选修4-5:不等式选讲
关于 的一元二次方程
的一元二次方程 对任意
对任意 无实根,求实数
无实根,求实数 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com