某市在“节约用水、保护水资源”的宣传教育活动中发布两则公益广告，活动组织者为了了解宣传效果，对10～60岁人群随机抽样调查了n人，要求被调查人回答两则广告的内容，调查结果如下表所示：

	广告一		广告二
年龄组	回答正确人数	在本组的频率	回答正确人数	在本组的频率
[10，20﹚	90	a	45	b
[20，30﹚	225	0.75	240	0.8
[30，40﹚	378	0.9	252	0.6
[40，50﹚	180	c	120	d
[50，60﹚	15	0.25	30	0.5

被抽样调查的n人在各年龄段人数的分布情况如频率分布直方图所示（如图）
（1）分布求出n和数表中a，b，c，d的值；
（2）如果表中的频率近似看作各年龄组中每人正确回答广告的概率，从被调查的n人中任选一人，求此人能正确回答广告一的概率；
（3）如果[10，20）年龄组中每人对两则广告都回答错误的概率为

3

8

，组织者随机请一名16岁的学生回答两则广告内容，求该学生至少能正确回答一个广告的概率．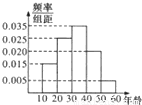

某大学高等数学老师上学期分别采用了A，B两种不同的教学方式对甲、乙两个大一新生班进行教改试验（两个班人数均为60人，入学数学平均分数和优秀率都相同；勤奋程度和自觉性都一样）．现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩，得到茎叶图如图：
（Ⅰ）从乙班这20名同学中随机抽取两名高等数学成绩不得低于85分的同学，求成绩为90分的同学被抽中的概率；
（Ⅱ）学校规定：成绩不低于85分的为优秀，请填写下面的2×2列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”

	甲班	乙班	合计
优秀
不优秀
合计

下面临界值表仅供参考：

P（K2≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式：K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

，其中n=a+b+c+d）
（Ⅲ）从乙班高等数学成绩不低于85分的同学中抽取2人，成绩不低于90分的同学得奖金100元，否则得奖金50元，记ξ为这2人所得的总奖金，求ξ的分布列和数学期望．