
题目列表(包括答案和解析)
| A、“集合的概念”的下位 | B、“集合的表示”的下位 | C、“基本关系”的下位 | D、“基本运算”的下位 |

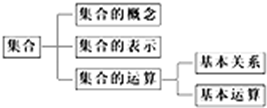
右图是集合的知识结构图,如果
要加入“补集”,则应该放在( )
A.“集合的概念”的下位
B.“集合的表示”的下位
C.“基本关系”的下位
D.“基本运算”的下位

当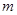 为何实数时,复数Z=
为何实数时,复数Z= 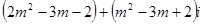 是
是
(1)实数;(2)虚数;(3)纯虚数;(4)对应点在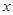 轴上方。
轴上方。
【解析】本试题主要是考查了复数的概念的运用。
如图是《集合》的知识结构图,如果要加入“交集”,则应该放在
| A.“集合的概念”的下位 |
| B.“集合的表示”的下位 |
| C.“基本关系”的下位 |
| D.“基本运算”的下位 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com