练习册

  • 练习册
  • 试题
    高考试题一般不要求特殊技巧.着重在“通性.通法 上.总结数学学科中解决问题的基本思想和方法.重点放在有价值的常规方法的应用上.特别是教材中每章节所给出的解决问题的一般方法． 【查看更多】

     

    题目列表(包括答案和解析)

    设函数fn( θ )=sinnθ+( -1 )ncosnθ，0≤θ≤
    π
    4
    ，其中n为正整数．
    （Ⅰ）判断函数f1（θ）、f3（θ）的单调性，并就f1（θ）的情形证明你的结论；
    （Ⅱ）证明：2f6（θ）-f4（θ）=（cos4θ-sin4θ）（cos2θ-sin2θ）；
    （Ⅲ）试给出求函数fn（θ）的最大值和最小值及取得最值时θ的取值的一般规律（不要求给出证明）．
    fn（θ） fn（θ）的
    单调性    		 fn（θ）的最小值及取得最小值时θ的取值 fn（θ）的最大值及取得最大值时θ的取值
    n=1
    n=2
    n=3
    n=4
    n=5
    n=6

    查看答案和解析>>

    (2013·上海高考)如图,已知双曲线C1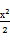：-y2=1,曲线C2：|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.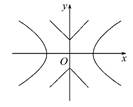

    (1)在正确证明C1的左焦点是“C1-C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证).
    (2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1-C2型点”.
    (3)求证：圆x2+y2=内的点都不是“C1-C2型点”.

    查看答案和解析>>

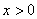     已知函数是在上每一点均可导的函数，若在时恒成立．

    （1）求证：函数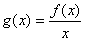在上是增函数；

    （2）求证：当时，有；

    （3）请将（2）问推广到一般情况，并证明你的结论（不要求证明）．

     

     

     

     

     

     

     

    查看答案和解析>>

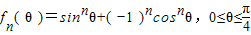    设函数，其中n为正整数．
    （Ⅰ）判断函数f1（θ）、f3（θ）的单调性，并就f1（θ）的情形证明你的结论；
    （Ⅱ）证明：2f6（θ）-f4（θ）=（cos4θ-sin4θ）（cos2θ-sin2θ）；
    （Ⅲ）试给出求函数fn（θ）的最大值和最小值及取得最值时θ的取值的一般规律（不要求给出证明）．
    fn（θ）fn（θ）的
    单调性    		fn（θ）的最小值及取得最小值时θ的取值fn（θ）的最大值及取得最大值时θ的取值
    n=1
    n=2
    n=3
    n=4
    n=5
    n=6

    查看答案和解析>>

       随着新课改的在我国的大力推行，过去一些陈旧的试题还不能更好地满足用户的需求。高考资源网将举办“新课改原创试题大比拼”，广大一线教师人人均可参与，只要参与就有机会。 “新课改原创试题大比拼”为您提供展示的平台，只要你有实力大奖就属于你！

    查看答案和解析>>


    同步练习册答案