
题目列表(包括答案和解析)
 如图,直线l⊥平面α,垂足为O,已知△ABC中,∠ABC为直角,AB=2,BC=1,该直角三角形做符合以下条件的自由运动:(1)A∈l,(2)B∈α.则C、O两点间的最大距离为
如图,直线l⊥平面α,垂足为O,已知△ABC中,∠ABC为直角,AB=2,BC=1,该直角三角形做符合以下条件的自由运动:(1)A∈l,(2)B∈α.则C、O两点间的最大距离为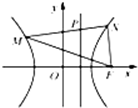 (2012•资阳三模)如图,直线l与双曲线C:
(2012•资阳三模)如图,直线l与双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 1 |
| 2 |
| p |
| 2 |
| p |
| 2 |
| QP |
| QF |
| FP |
| FQ |
 (2007•武汉模拟)如图,直线l:y=
(2007•武汉模拟)如图,直线l:y=| 4 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 12 |
| 11 |
| b |
| a |
 如图,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它扫过△AOB 所得图形的面积为s,它与x轴的交点为(x,0).
如图,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它扫过△AOB 所得图形的面积为s,它与x轴的交点为(x,0).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com