
题目列表(包括答案和解析)
 (m>0,n>0且m≠n)的两个焦点.
(m>0,n>0且m≠n)的两个焦点. )到两个焦点的距离之和等于4,求椭圆C的方程.
)到两个焦点的距离之和等于4,求椭圆C的方程. ,求△PF1F2的面积.
,求△PF1F2的面积. (a>0,b>0)是否具有类似的性质?并证明你的结论.通过对上面问题进一步研究,请你概括具有上述性质的二次曲线更为一般的结论,并说明理由.
(a>0,b>0)是否具有类似的性质?并证明你的结论.通过对上面问题进一步研究,请你概括具有上述性质的二次曲线更为一般的结论,并说明理由.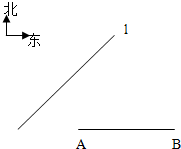 如图,某开发区旁边有一条东北走向的公路l,开发区内有两工厂A,B(B在A正东4km),A工厂到公路l的距离为(
如图,某开发区旁边有一条东北走向的公路l,开发区内有两工厂A,B(B在A正东4km),A工厂到公路l的距离为(| 6 |
| 2 |
| 2 |
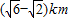 .建立适当的坐标系,解决下列问题:
.建立适当的坐标系,解决下列问题: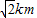 ,在(Ⅱ)中的环行公路上设一站点N,使站点N到C,B两地的距离之和最小.试问:满足要求的点N在什么位置(不要证明),并求|NC|+|NB|的值.
,在(Ⅱ)中的环行公路上设一站点N,使站点N到C,B两地的距离之和最小.试问:满足要求的点N在什么位置(不要证明),并求|NC|+|NB|的值.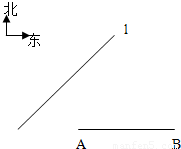
| x2 |
| m2 |
| y2 |
| n2 |
| 3 |
| 2 |
| PF1 |
| PF2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| m2 |
| y2 |
| n2 |
| 3 |
| 2 |
| PF1 |
| PF2 |
| x2 |
| a2 |
| y2 |
| b2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com