
题目列表(包括答案和解析)
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当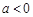 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
 10、如图表示一位骑自行车者和一位骑摩托车者在相距80km的两城镇间旅行的函数图象,由图可知:骑自行车者用了6小时,沿途休息了1小时,骑摩托车者用了2小时.根据这个函数图象,提出关于这两个旅行者的如下信息:
10、如图表示一位骑自行车者和一位骑摩托车者在相距80km的两城镇间旅行的函数图象,由图可知:骑自行车者用了6小时,沿途休息了1小时,骑摩托车者用了2小时.根据这个函数图象,提出关于这两个旅行者的如下信息: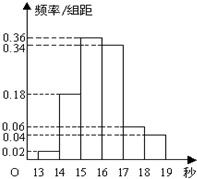 某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于19秒.右图是按上述分组方法得到的频率分布直方图.由图可知,人数最多的一组是第
某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于19秒.右图是按上述分组方法得到的频率分布直方图.由图可知,人数最多的一组是第| 季度 | 1 | 2 | 3 | 4 |
| x | 30 | 31 | 33 | 34 |
| y | 18 | 16 | 14 | 12 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com