
题目列表(包括答案和解析)
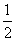 的定义域是[n,n+1](n∈N),问f(x)的值域中有多少个整数?
的定义域是[n,n+1](n∈N),问f(x)的值域中有多少个整数? (1)求函数f(x)的最大值和最小值;
(2)试比较f(![]() )与
)与![]() +2的大小;
+2的大小;
(3)某同学发现:当x=![]() (n∈N)时,有f(x)<2x+2,由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由.
(n∈N)时,有f(x)<2x+2,由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由.
①对于任意x∈[0,1],总有f(x)≥3,且f(1)=4;
②若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-3.
(1)求f(0)的值;
(2)求证:f(x)≤4;
(3)当x∈(![]() ](n=1,2,3,…)时,试证明f(x)<3x+3.
](n=1,2,3,…)时,试证明f(x)<3x+3.
(文)如图,设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A、B两点,且A、B两点坐标为(x1,y1)、(x2,y2),y1>0,y2<0,P是此抛物线的准线上的一点,O是坐标原点.

(1)求证:y1y2=-p2;
(2)直线PA、PF、PB的方向向量为(1,a)、(1,b)、(1,c),求证:实数a、b、c成等差数列;
(3)若![]() =0,∠APF=α,∠BPF=β,∠PFO=θ,求证:θ=|α-β|.
=0,∠APF=α,∠BPF=β,∠PFO=θ,求证:θ=|α-β|.
(1)如果函数y=x+![]() (x>0)的值域为[6,+∞),求b的值;
(x>0)的值域为[6,+∞),求b的值;
(2)研究函数y=x2+![]() (常数c>0)在定义域内的单调性,并说明理由;
(常数c>0)在定义域内的单调性,并说明理由;
(3)对函数y=x+![]() 和y=x2+
和y=x2+![]() (常数a>0)作出推广,使它们都是你所推广的函数的特例,研究推广后的函数的单调性(只须写出结论,不必证明),并求函数f(x)=(x2+
(常数a>0)作出推广,使它们都是你所推广的函数的特例,研究推广后的函数的单调性(只须写出结论,不必证明),并求函数f(x)=(x2+![]() )n+(
)n+(![]() +x)n(n是正整数)在区间[
+x)n(n是正整数)在区间[![]() ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).
(1)试求函数f(x)的最大值和最小值;
(2)试比较f(![]() n)与
n)与![]() n+2的大小(n∈N);
n+2的大小(n∈N);
(3)某人发现:当x=![]() n(n∈N)时,有f(x)<2x+2.由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由.
n(n∈N)时,有f(x)<2x+2.由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com