设双曲线的两个焦点分别为、，离心率为2．

（1）求双曲线的渐近线方程；

（2）过点能否作出直线，使与双曲线交于、两点，且，若存在，求出直线方程，若不存在，说明理由．

【解析】(1)根据离心率先求出a²的值，然后令双曲线等于右侧的1为0，解此方程可得双曲线的渐近线方程.

（2）设直线l的方程为,然后直线方程与双曲线方程联立，消去y，得到关于x的一元二次方程，利用韦达定理表示此条件，得到关于k的方程，解出k的值，然后验证判别式是否大于零即可.

已知直线：Ax＋By＋C=0()，点在上，则的方程可化为

[　　]

A．

B．

C．

D．

已知直线：Ax＋By＋C=0()，点在上，则的方程可化为

[　　]

A．

B．

C．

D．

已知函数，.

（Ⅰ）若函数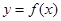依次在处取到极值.求的取值范围；

（Ⅱ）若存在实数，使对任意的，不等式 恒成立.求正整数的最大值.

【解析】第一问中利用导数在在处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。

第二问中，利用存在实数，使对任意的，不等式 恒成立转化为，恒成立，分离参数法求解得到范围。

解：（1）

①

（2）不等式 ，即，即.

转化为存在实数，使对任意的，不等式恒成立.

即不等式在上恒成立.

即不等式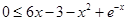在上恒成立.

设，则.

设，则，因为，有.

故在区间上是减函数。又

故存在，使得.

当时，有，当时，有.

从而在区间上递增，在区间上递减.

又[来源:]

所以当时，恒有；当时，恒有；

故使命题成立的正整数m的最大值为5

已知函数．

（1）试求的值域；

(2)设，若对， ，恒 成立，试求实数的取值范围

【解析】第一问利用

第二问中若，则，即当时，，又由（Ⅰ）知

若对，，恒有成立，即转化得到。

解：（1）函数可化为,  ……5分

 (2) 若，则，即当时，，又由（Ⅰ）知．        …………8分

若对，，恒有成立，即，

，即的取值范围是