
题目列表(包括答案和解析)
(2012年高考(重庆文))(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分))已知![]()
![]() 为等差数列,且
为等差数列,且![]() (Ⅰ)求数列
(Ⅰ)求数列![]() 的通项公式;(Ⅱ)记
的通项公式;(Ⅱ)记![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 成等比数列,求正整数
成等比数列,求正整数![]() 的值.
的值.
(本小题满分12分)
某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| | 60分以下 | 61-70分 | 71-80分 | 81-90分 | 91-100分 |
| 甲班(人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人数) | 4 | 8 | 13 | 15 | 10 |
| | 优秀人数 | 非优秀人数 | 合计 |
| 甲班 | | | |
| 乙班 | | | |
| 合计 | | | |
(本小题满分12分)
某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解,训练对提髙‘数学应用题得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| 60分以下 | 61—70 分 | 71—80 分 | 81-90 分 | 91-100分 | |
| 甲班(人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人数) | 8 | 13 | 15 | 10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(I )试分别估计两个班级的优秀率;
(II)由以上统计数据填写下面2 X 2列联表,并问是否有"5匁的把握认为“加强‘语文阅读理解’训练对提商‘数学应用题’得分率”有帮助.
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | |||
| 乙班 | |||
| 合计 |
参考公式及数据:![]() ,
,
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0. 05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.82 |
从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图所示,观察图形,回答下列问题:
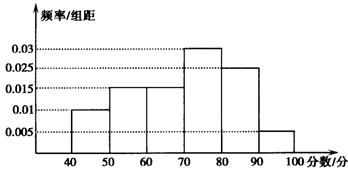
⑴80~90这一组的频数、频率分别是多少?
⑵估计这次环保知识竞赛的及格率(60分及以上为及格). (本小题满分10分)
【解析】本试题主要考查了统计和概率的综合运用。
第一问频率:0.025×10=0.25;……………3分
频数:60×0.25=15. ………………6分
第二问0.015×10+0.025×10+0.03×10+0.005×10=0.75
解:(1)频率:0.025×10=0.25;……………3分
频数:60×0.25=15. ………………6分
(2)0.015×10+0.025×10+0.03×10+0.005×10=0.75
(本小题满分12分)
某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解,训练对提髙‘数学应用题得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| 60分以下 | 61—70 分 | 71—80 分 | 81-90 分 | 91-100分 | |
| 甲班(人数) | 3 | 6 | 11 | 18 | 12 |
| 乙班(人数) | 8 | 13 | 15 | 10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(I )试分别估计两个班级的优秀率;
(II)由以上统计数据填写下面2 X 2列联表,并问是否有"5匁的把握认为“加强‘语文阅读理解’训练对提商‘数学应用题’得分率”有帮助.
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | |||
| 乙班 | |||
| 合计 |
参考公式及数据:![]() ,
,
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0. 05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.82 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com