
题目列表(包括答案和解析)
蒲丰(Buffon)投针问题:平面上画很多平行线,间距均为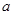 ,向此平面投掷长为
,向此平面投掷长为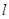 (
(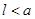 )的针,则此针与任一平行线相交的概率为
。
)的针,则此针与任一平行线相交的概率为
。


图1-1-17 图1-1-18
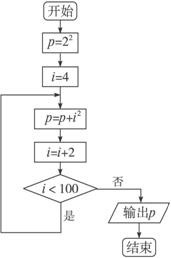

图1-1-19 图1-1-20
(1)其中正确的流程图有哪几个?错误的流程图有哪几个?错误的指出错在哪里.
(2)在错误的程序流程图中,所说的算法能运行到底吗?若能,输出的结果是什么?
(3)根据上面的回答总结出应用循环结构应该注意什么问题?
蒲丰(Buffon)投针问题:平面上画很多平行线,间距均为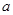 ,向此平面投掷长为
,向此平面投掷长为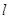 (
(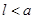 )的针,则此针与任一平行线相交的概率为 。
)的针,则此针与任一平行线相交的概率为 。
| x2 |
| a2 |
| y2 |
| b2 |
|
| π |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com