
题目列表(包括答案和解析)
 [必做题]利用空间向量的方法解决下列问题:在正方体ABCD-A1B1C1D1中,E,F分别是BB1,DC的中点.
[必做题]利用空间向量的方法解决下列问题:在正方体ABCD-A1B1C1D1中,E,F分别是BB1,DC的中点.| i |
| j |
| k |
| a |
| i |
| j |
| k |
| b |
| i |
| j |
| k |
| a |
| b |
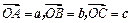 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若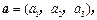
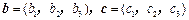 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算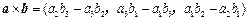 ,显然
,显然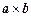 的结果仍为一向量,记作
的结果仍为一向量,记作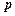 .
.
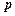 为平面
为平面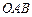 的法向量;
的法向量;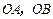 为边的平行四边形
为边的平行四边形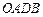 的面积等于
的面积等于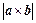 ;
;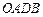 按向量
按向量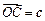 平移,得到一个平行六面体
平移,得到一个平行六面体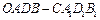 ,试判断平行六面体的体积
,试判断平行六面体的体积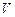 与
与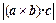 的大小.
的大小.下面几种推理是类比推理的是 ( )
A.两条直线平行,同旁内角互补,如果 和 和 是两条平行直线的同旁内角,则 是两条平行直线的同旁内角,则  |
| B.由平面向量的运算性质,推测空间向量的运算性质 |
| C.某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员,; |
D.一切偶数都能被2整除, 是偶数,所以 是偶数,所以 能被2整除 能被2整除 |
下面几种推理是类比推理的是( )
A.两条直线平行,同旁内角互补,如果 和
和 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则
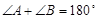
B.由平面向量的运算性质,推测空间向量的运算性质
C.某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员
D.一切偶数都能被2整除, 是偶数,所以
是偶数,所以 能被2整除
能被2整除
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com