练习册

  • 练习册
  • 试题
    21．解:(I) 0 (0.1) 1 (1.3) 3 + 0 - 0 1 4分 (II)设时.函数的值域为A. . 总存在 (1)当时. 上单调递减. ----------8分 (2)当时. 令 ①当时.列表如下: 0 3 - 0 + 0 若. 则 ------------ 11分 ②当时.时. 函数上单调递减 -------- 13分 综上.实数的取值范围是 ---------- 14分 【查看更多】

     

    题目列表(包括答案和解析)

    已知 S=1+（1+3）+（1+3+5）+（1+3+5+7）+…+（1+3+5+…+199）
    （Ⅰ）下面给出求S的算法，请将空白部分补充完整；
    （Ⅱ）请将求S的流程图补充完整，内容直接填在程序框图中；
    解：（Ⅰ）算法分析：（1）S=0，T=0，i=1；
    （2）将T+2i-1赋值给T，将S+T赋值给S；
    （3）将
     
    赋值给i；
    （4）
     
    ；
    （5）输出S，结束运算．
    （Ⅱ）流程图：
    精英家教网

    查看答案和解析>>

    已知S=1+（1+3）+（1+3+5）+（1+3+5+7）+…+（1+3+5+…+199）
    （Ⅰ）下面给出求S的算法，请将空白部分补充完整；
    （Ⅱ）请将求S的流程图补充完整，内容直接填在程序框图中；
    解：（Ⅰ）算法分析：（1）S=0，T=0，i=1；
    （2）将T+2i-1赋值给T，将S+T赋值给S；
    （3）将______赋值给i；
    （4）______；
    （5）输出S，结束运算．
    （Ⅱ）流程图：

    查看答案和解析>>

    在复平面内， 是原点，向量对应的复数是，=2+i。

    （Ⅰ）如果点A关于实轴的对称点为点B，求向量对应的复数和；

    （Ⅱ）复数，对应的点C，D。试判断A、B、C、D四点是否在同一个圆上？并证明你的结论。

    【解析】第一问中利用复数的概念可知得到由题意得，A（2,1）  ∴B(2,-1)   ∴  =(0,-2) ∴=-2i  ∵ （2+i）(-2i)=2-4i,      ∴  =

    第二问中，由题意得，=（2,1）  ∴

    同理，所以A、B、C、D四点到原点O的距离相等，

    ∴A、B、C、D四点在以O为圆心，为半径的圆上

    （Ⅰ）由题意得，A（2,1）  ∴B(2,-1)   ∴  =(0,-2) ∴=-2i     3分

         ∵ （2+i）(-2i)=2-4i,      ∴  =                 2分

    （Ⅱ）A、B、C、D四点在同一个圆上。                              2分

    证明：由题意得，=（2,1）  ∴

      同理，所以A、B、C、D四点到原点O的距离相等，

    ∴A、B、C、D四点在以O为圆心，为半径的圆上

     

    查看答案和解析>>

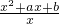    已知f（x）=数学公式（x∈（0，+∞）），存在实数a，b，使f（x）满足：（i）f（x）在（0，2]上是减函数，在[2，+∞）是增函数；
    （ii）f（x）的最小值是5．
    （1）求a，b的值及f（x）的解析式；
    （2）（理科）求y=f（x）的图象与三直线x=1，x=e及y=0所围成的图形面积；
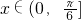    （3）若函数F（x）=f（x）-c•cosx，当数学公式时是单调减函数，求实数c的取值范围．

    查看答案和解析>>

    定义：F（x，y）=yx（x＞0，y＞0）
    （1）解关于x的不等式F（1，x2）+F（2，x）≤3x-1；
    （2）记f（x）=3•F（1，x），设Sn=f(
    1
    n
    )+f(
    2
    n
    )+f(
    3
    n
    )+…+f(
    n
    n
    )    ，若不等式
    an
    Sn
    ＜
    an+1
    Sn+1
    对n∈N*恒成立，求实数a的取值范围；
    （3）记g（x）=F（x，2），正项数列an满足：a1=3，g(an+1)=8an，求数列an的通项公式，并求所有可能的乘积ai•aj（1≤i≤j≤n）的和．

    查看答案和解析>>


    同步练习册答案