
题目列表(包括答案和解析)
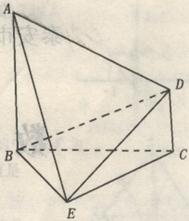
如图,已知![]() 平面
平面![]() 是正三角
是正三角
形,![]() 。
。
(Ⅰ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?
?
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的正切值。
的正切值。
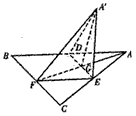
(如图)已知四棱锥S-ABCD的底面ABCD是菱形,将面SAB,SAD,ABCD 展开成平面后的图形恰好为一正三角形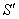 SC.
SC.
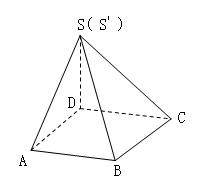
(1)求证:在四棱锥S-ABCD中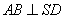 。
。
(2)若AC长等于6,求异面直线AB与SC之间的距离。
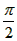 ]
]
(09年丰台区二模文)(14分)
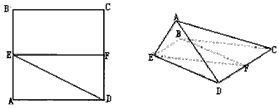
如图,正△ABC的中线AF与中位线DE相交于点G,![]() 已知△A′DE是△AED绕边DE旋转过程中的一个图形。
已知△A′DE是△AED绕边DE旋转过程中的一个图形。
(I)求证点A′在平面ABC上的射影在线段AF上;
(II)当二面角A′―DE―A为60°时,求三棱锥A′―FED的体积。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com