
题目列表(包括答案和解析)
当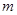 为何实数时,复数Z=
为何实数时,复数Z= 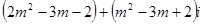 是
是
(1)实数;(2)虚数;(3)纯虚数;(4)对应点在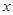 轴上方。
轴上方。
【解析】本试题主要是考查了复数的概念的运用。
已知 是等差数列,其前n项和为
是等差数列,其前n项和为 ,
,  是等比数列,且
是等比数列,且


(I)求数列 与
与 的通项公式;
的通项公式;
(II)记 求证:
求证: ,
, 。
。
【考点定位】本小题主要考查等差数列与等比数列的概念、通项公式、前n项和公式、数列求和等基础知识.考查化归与转化的思想方法.考查运算能力、推理论证能力.
已知曲线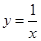 和
和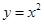 相交于点A,
相交于点A,
(1)求A点坐标;
(2)分别求它们在A点处的切线方程(写成直线的一般式方程);
(3)求由曲线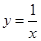 在A点处的切线及
在A点处的切线及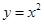 以及
以及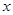 轴所围成的图形面积。(画出草图)
轴所围成的图形面积。(画出草图)
【解析】本试题主要考察了导数的几何意义的运用,以及利用定积分求解曲边梯形的面积的综合试题。先确定切点,然后求解斜率,最后得到切线方程。而求解面积,要先求解交点,确定上限和下限,然后借助于微积分基本定理得到。
已知函数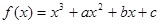 ,曲线
,曲线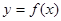 在点x=1处的切线为
在点x=1处的切线为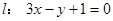 ,若
,若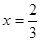 时,
时,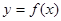 有极值。
有极值。
(1)求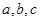 的值;
(2)求
的值;
(2)求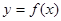 在
在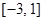 上的最大值和最小值。
上的最大值和最小值。
【解析】本试题主要考查了导数的几何意义的运用,以及运用导数在研究函数的极值和最值的问题。体现了导数的工具性的作用。
 是等差数列,其前n项和为
是等差数列,其前n项和为 ,
,  是等比数列,且
是等比数列,且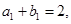


 与
与 的通项公式;
的通项公式; 求证:
求证: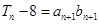 ,
, 。
。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com