
题目列表(包括答案和解析)
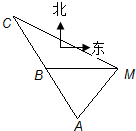 (2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )
(2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )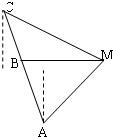 如图,已知A、B、C是一条直路上的三点,AB与BC各等于1千米,从三点分别遥望塔M,在A处看见塔在北偏东45方向,在B处看见塔在正东方向,在C处看见塔在南偏东60°方向,求塔到直路ABC的最短距离.
如图,已知A、B、C是一条直路上的三点,AB与BC各等于1千米,从三点分别遥望塔M,在A处看见塔在北偏东45方向,在B处看见塔在正东方向,在C处看见塔在南偏东60°方向,求塔到直路ABC的最短距离. (2011•江西模拟)如图,已知A是椭圆
(2011•江西模拟)如图,已知A是椭圆| x2 |
| a2 |
| y2 |
| b2 |
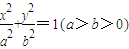 上的一个动点,F1,F2分别为椭圆的左、右焦点,弦AB过点F2,当AB⊥x轴时,恰好有|AF1|=3|AF2|.
上的一个动点,F1,F2分别为椭圆的左、右焦点,弦AB过点F2,当AB⊥x轴时,恰好有|AF1|=3|AF2|.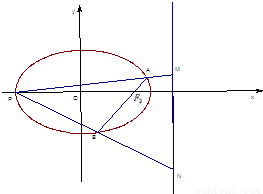

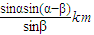
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com