
题目列表(包括答案和解析)
物理学家James.D.Forbes试图通过水的沸点来估计海拔高度,他知道通过气压计测得的大气压可用于得到海拔高度,气压越低,高度越高,他测量了17个地方水的沸点(℉)及大气压数据,并且对数据作了简单的处理,得到了较为明确的数学关系,所提数据如下:
|
测点编号 |
沸点(℉) |
气压 |
1g(气压) |
100´1g(气压) |
|
1 |
194.5 |
20.79 |
1.3179 |
131.79 |
|
2 |
194.3 |
20.79 |
1.3179 |
131.79 |
|
3 |
197.9 |
22.40 |
1.3502 |
135.02 |
|
4 |
198.4 |
22.67 |
1.3555 |
135.55 |
|
5 |
199.4 |
23.15 |
1.3646 |
136.46 |
|
6 |
199.9 |
23.35 |
1.3683 |
136.83 |
|
7 |
200.9 |
23.89 |
1.3782 |
137.82 |
|
8 |
201.1 |
23.99 |
1.3800 |
138.00 |
|
9 |
201.4 |
24.02 |
1.3805 |
138.05 |
|
10 |
201.3 |
24.01 |
1.3806 |
138.06 |
|
11 |
203.6 |
25.14 |
1.4004 |
140.04 |
|
12 |
204.6 |
26.57 |
1.4244 |
142.44 |
|
13 |
209.5 |
28.49 |
1.4547 |
145.47 |
|
15 |
208.6 |
27.76 |
1.4434 |
144.34 |
|
15 |
210.7 |
29.04 |
1.4630 |
146.30 |
|
16 |
211.9 |
29.88 |
1.4754 |
147.54 |
|
17 |
212.2 |
30.06 |
1.4780 |
147.80 |
(1)试作出气压y=100´1g(气压)关于沸点(℉)的散点图;
(2)根据散点图判断变量x与y的相关关系;计算变量x与y的相关系数;
(3)建立变量x与y的一元线性回归方程。
|
测点编号 |
沸点(℉) |
气压 |
1g(气压) |
100´1g(气压) |
|
1 |
194.5 |
20.79 |
1.3179 |
131.79 |
|
2 |
194.3 |
20.79 |
1.3179 |
131.79 |
|
3 |
197.9 |
22.40 |
1.3502 |
135.02 |
|
4 |
198.4 |
22.67 |
1.3555 |
135.55 |
|
5 |
199.4 |
23.15 |
1.3646 |
136.46 |
|
6 |
199.9 |
23.35 |
1.3683 |
136.83 |
|
7 |
200.9 |
23.89 |
1.3782 |
137.82 |
|
8 |
201.1 |
23.99 |
1.3800 |
138.00 |
|
9 |
201.4 |
24.02 |
1.3805 |
138.05 |
|
10 |
201.3 |
24.01 |
1.3806 |
138.06 |
|
11 |
203.6 |
25.14 |
1.4004 |
140.04 |
|
12 |
204.6 |
26.57 |
1.4244 |
142.44 |
|
13 |
209.5 |
28.49 |
1.4547 |
145.47 |
|
15 |
208.6 |
27.76 |
1.4434 |
144.34 |
|
15 |
210.7 |
29.04 |
1.4630 |
146.30 |
|
16 |
211.9 |
29.88 |
1.4754 |
147.54 |
|
17 |
212.2 |
30.06 |
1.4780 |
147.80 |
(1)试作出气压y=100´1g(气压)关于沸点(℉)的散点图;
(2)根据散点图判断变量x与y的相关关系;计算变量x与y的相关系数;
(3)建立变量x与y的一元线性回归方程。
已知向量 (
( ),向量
),向量 ,
, ,
,
且

 .
.
(Ⅰ)求向量 ;
(Ⅱ)若
;
(Ⅱ)若 ,
, ,求
,求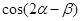 .
.
【解析】本试题主要考查了向量的数量积的运算,以及两角和差的三角函数关系式的运用。
(1)问中∵ ,∴
,∴ ,…………………1分
,…………………1分
∵ ,得到三角关系是
,得到三角关系是 ,结合
,结合 ,解得。
,解得。
(2)由 ,解得
,解得 ,
, ,结合二倍角公式
,结合二倍角公式 ,和
,和 ,代入到两角和的三角函数关系式中就可以求解得到。
,代入到两角和的三角函数关系式中就可以求解得到。
解析一:(Ⅰ)∵ ,∴
,∴ ,…………1分
,…………1分
∵ ,∴
,∴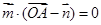 ,即
,即 ① …………2分
① …………2分
又 ② 由①②联立方程解得,
② 由①②联立方程解得,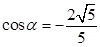 ,
,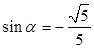 5分
5分
∴ ……………6分
……………6分
(Ⅱ)∵ 即
即 ,
, , …………7分
, …………7分
∴ ,
, ………8分
………8分
又∵ , ………9分
, ………9分
 , ……10分
, ……10分
∴ .
.
解法二: (Ⅰ) ,…………………………………1分
,…………………………………1分
又 ,∴
,∴ ,即
,即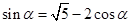 ,①……2分
,①……2分
又 ②
②
将①代入②中,可得 ③ …………………4分
③ …………………4分
将③代入①中,得 ……………………………………5分
……………………………………5分
∴ …………………………………6分
…………………………………6分
(Ⅱ) 方法一
∵ ,
, ,∴
,∴ ,且
,且 ……7分
……7分
∴ ,从而
,从而 . …………………8分
. …………………8分
由(Ⅰ)知 ,
,
 ; ………………9分
; ………………9分
∴ . ………………………………10分
. ………………………………10分
又∵ ,∴
,∴ ,
又
,
又 ,∴
,∴ ……11分
……11分
综上可得  ………………………………12分
………………………………12分
方法二∵ ,
, ,∴
,∴ ,且
,且 …………7分
…………7分
∴ .
……………8分
.
……………8分
由(Ⅰ)知 ,
, .
…………9分
.
…………9分
∴ ……………10分
……………10分
∵ ,且注意到
,且注意到 ,
,
∴ ,又
,又 ,∴
,∴ ………………………11分
………………………11分
综上可得  …………………12分
…………………12分
(若用 ,又∵
,又∵ ∴
∴  ,
,
三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共76分)。
17.(12分)以下资料是一位销售经理收集来的每年销售额和销售经验年数的关系:
|
销售经验(年) |
1 |
3 |
4 |
4 |
6 |
8 |
10 |
10 |
11 |
13 |
|
年销售额(千元) |
80 |
97 |
92 |
102 |
103 |
111 |
119 |
123 |
117 |
136 |
(1)依据这些数据画出散点图并作直线 =78+4.2x,计算
=78+4.2x,计算 (yi-
(yi- i)2;
i)2;
(2)依据这些数据由最小二乘法求线性回归方程,并据此计算 ;
;
(3)比较(1)和(2)中的残差平方和 的大小.
的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com