
题目列表(包括答案和解析)
A、P1=
| ||||||
B、P1=
| ||||||
C、P1=
| ||||||
D、P1=
|
A.P1=
| B.P1=
| ||||||||||||
C.P1=
| D.P1=
|
 P2=
P2= P3=
P3=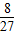
 P2=
P2=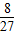 P3=
P3=
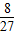 P2=
P2= P3=
P3=
 P2=
P2= P3=
P3=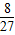
 P2=
P2= P3=
P3=
 P2=
P2= P3=
P3=
 P2=
P2= P3=
P3=
 P2=
P2= P3=
P3=
口袋里装有红球、白球、黑球各
1个,这3个球除颜色外完全相同,有放回地连续抽取2次,每次从中任意地取出1个球,计算下列事件的概率:(1)
取出的球全是红球;(2)
取出的球不全是红球;(3)
取出的球中至少有1个是红球;(4)
取出的球是同一颜色;(5)
取出的球颜色不同.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com