
题目列表(包括答案和解析)
(2)描述法:把集合中的元素 的描述出来,写在 内表示集合的方法.一般形式是{x|p},其中竖线前面的x叫做此集合的代表元素,竖线后面的p指出元素x所具有的公共属性.描述法便于从整体上把握一个集合,常适用于集合中元素的公共属性较为明显时.
(3)韦恩图:为了形象地表示集合,有时常用一些封闭的 表示一个集合,这样的图形称为韦恩图,在解题时,利用韦恩图“数”和“形”结合,使得解答十分直观.?
如集合A={a,b,c}可形象地表示为图(1)或图(2).?
(1) (2)
你以前听说过“鸡兔同笼”问题吗?这个问题,是我国古代著名趣题之一.大约在1 500年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚.求笼中各有几只鸡和兔?
你会解答这个问题吗?你想知道《孙子算经》中是如何解答这个问题的吗?
解答思路是这样的:假如砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独角鸡”,每只兔就变成了“双脚兔”.这样,(1)鸡和兔的脚的总数就由94只变成了47只;(2)如果笼子里有一只兔子,则脚的总数就比头的总数多1.因此,脚的总只数47与总头数35的差,就是兔子的只数,即47-35=12(只).显然,鸡的只数就是35-12=23(只)了.
这一思路新颖而奇特,其“砍足法”也令古今中外数学家赞叹不已.这种思维方法叫化归法.
化归法就是在解决问题时,先不对问题采取直接的分析,而是将题中的条件或问题进行变形,使之转化,直到最终把它归成某个已经解决的问题.
1.古代《孙子算经》就有这么好的解法——化归法,这一思路新颖而奇特,其“砍足法”也令古今中外数学家赞叹不已.对此,谈谈你的看法.
2.我国古代数学研究一直处于领先地位,现在有所落后了,对此,我们不应只感叹古人的伟大,而更应该树立为科学而奋斗终身的信心,同学们,你们准备好了吗?
| z1-1 |
| z1+1 |
| t | ||
|
| A、当α在一、二象限取正,在三、四象限取负 |
| B、当α在一、四象限取正,在二、三象限取负 |
| C、在α在一、三象限取正,在二、四象限取负 |
| D、当α仅在第一象取取正 |
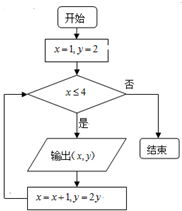 (2013•房山区二模)执行如图所示的程序框图.则输出的所有点(x,y)( )
(2013•房山区二模)执行如图所示的程序框图.则输出的所有点(x,y)( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com