杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果，它的许多性质与组合数的性质有关，杨辉三角中蕴藏了许多优美的规律．如图所示是一个11阶杨辉三角：

（1）求第20行中从左到右的第4个数；
（2）若第n行中从左到右第14与第15个数的比为

2

3

，求n的值；
（3）在第3斜列中，前5个数依次为1，3，6，10，15；第4斜列中，第5个数为35．显然，1+3+6+10+15=35．事实上，一般地有这样的结论：第m斜列中（从右上到左下）前k个数之和，一定等于第m+1斜列中第k个数．试用含有m，k（m，k∈N^*）的数学公式表示上述结论，并给予证明．

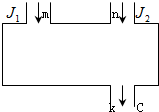如图所示是一个计算机程序运行装置示意图，J₁，J₂是数据入口，C是计算结果出口，计算过程是：由J₁，J₂分别输入正整数m和n，经过计算后得出的正整数k由C输出．此种计算装置完成的计算满足：①若J₁，J₂分别输入1，则输出结果为1；②若J₁输入任意固定的正整数，J₂输入的正整数增加1，则输出的结果比原来增加2；③若J₂输入1，J₁输入的正整数增加1，则输出结果为原来的2倍，试问：
（1）若J₁输入1，J₂输入正整数n，输出结果为多少？
（2）若J₂输入1，J₁输入正整数m，输出结果为多少？
（3）若J₁输入正整数m，J₂输入正整数n，输出结果为多少？

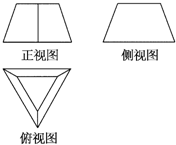如图所示是一个空间几何体的三视图，试用斜二测画法画出它的直观图（尺寸不限）．

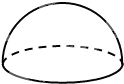如图所示是一个半径等于2的半球，现过半球底面的中心作一个与底面成90°的截面，则此截面的面积为（　　）

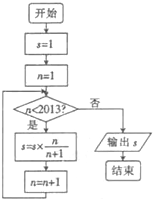如图所示是一个箅法的流程图，则输出s的值是．