
题目列表(包括答案和解析)
【必做题】本题满分10分.解答时应写出文字说明、证明过程或演算步骤.
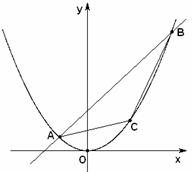
已知直线![]() 被抛物线
被抛物线![]() 截得的弦长
截得的弦长![]() 为20,
为20,![]() 为坐标原点.
为坐标原点.
(1)求实数![]() 的值;
的值;
(2)问点![]() 位于抛物线弧
位于抛物线弧![]() 上何处时,△
上何处时,△![]() 面积最大?
面积最大?
【必做题】本题满分10分.解答时应写出文字说明、证明过程或演算步骤.
甲、乙、丙三个同学一起参加某高校组织的自主招生考试,考试分笔试和面试两部分,笔试和面试均合格者将成为该高校的预录取生(可在高考中加分录取),两次考试过程相互独立.根据甲、乙、丙三个同学的平时成绩分析,甲、乙、丙三个同学能通过笔试的概率分别是0.6,0.5,0.4,能通过面试的概率分别是0.5,0.6,0.75.
(1)求甲、乙、丙三个同学中恰有一人通过笔试的概率;
(2)设经过两次考试后,能被该高校预录取的人数为![]() ,求随机变量
,求随机变量![]() 的期望
的期望![]() .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com