
题目列表(包括答案和解析)
(本小题15分)
先阅读下列不等式的证法,再解决后面的问题:已知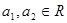 且
且 ,求证
,求证
证明:构造函数 因为对一切
因为对一切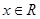 ,恒有
,恒有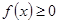 ,所以
,所以 4-8
4-8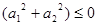 ,从而
,从而
(1)若 ,且
,且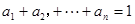 ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你的结论加以证明;
(3)若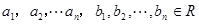 ,求证
,求证
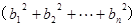
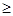
 .[
.[
已知△ 中,
中, ,求证
,求证 .
.
证明: ,
, ,画线部分是演绎推理的是()
,画线部分是演绎推理的是()
A.大前提 B.小前提 C.结论 D.三段论
已知△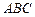 中,
中,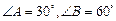 ,求证
,求证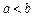 .
.
证明: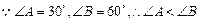 ,
,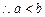 ,画线部分是演绎推理的是()
,画线部分是演绎推理的是()
| A.大前提 | B.小前提 | C.结论 | D.三段论 |
(本小题15分)
先阅读下列不等式的证法,再解决后面的问题:已知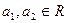 且
且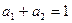 ,求证
,求证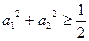
证明:构造 函数
函数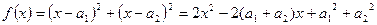 因为对一切
因为对一切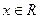 ,恒有
,恒有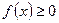 ,所以
,所以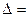 4-8
4-8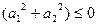 ,从而
,从而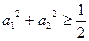
(1)若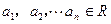 ,且
,且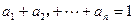 ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你的结论加以证明;
(3)若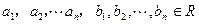 ,求证
,求证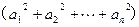
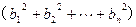
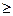
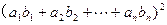 .[
.[
| C | m n |
| n |
| m |
| C | m-1 n-1 |
| (1+x)[1-(1+x)n] |
| 1-(1+x) |
| (1+x)n+1-(1+x) |
| x |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com