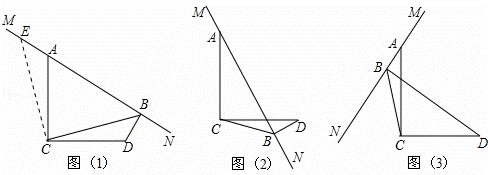
已知∠ACD=90°，MN是过点A的直线，AC=DC，DB⊥MN于点B，如图（1）．易证BD+AB=CB，过程如下：

过点C作CE⊥CB于点C，与MN交于点E

∵∠ACB+∠BCD=90°，∠ACB+∠ACE=90°，∴∠BCD=∠ACE．

∵四边形ACDB内角和为360°，∴∠BDC+∠CAB=180°．

∵∠EAC+∠CAB=180°，∴∠EAC=∠BDC．

又∵AC=DC，∴△ACE≌△DCB，∴AE=DB，CE=CB，∴△ECB为等腰直角三角形，∴BE=CB．

又∵BE=AE+AB，∴BE=BD+AB，∴BD+AB=CB．

（1）当MN绕A旋转到如图（2）和图（3）两个位置时，BD、AB、CB满足什么样关系式，请写出你的猜想，并对图（2）给予证明．

（2）MN在绕点A旋转过程中，当∠BCD=30°，BD=时，则CD=　2　，CB=　+1　．

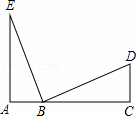
如图，已知BC=EC，∠BCE=∠ACD，要使△ABC≌△DEC，则应添加的一个条件为　AC=CD　．（答案不唯一，只需填一个）

如图，A，B，C三点在同一条直线上，∠A=∠C=90°，AB=CD，请添加一个适当的条件　AE=CB　，使得△EAB≌△BCD．

　　如图所示，AF、AC、DF、DB、EC都是直线，∠1=∠2，∠C=∠D，根据下列推理，在括号内填写理由．

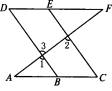
　　∵　∠1=∠2(　)，∠1=∠3(　)，∴　∠2=∠3(　)．

　　∴　DB∥EC(　)

　　∴　∠C=∠ABD(　)

　　又∵　∠C=∠D(　)，∴　∠D=∠ABD(　)．

　　∴　AC∥DF(　)．∴　∠A=∠F(　)．

如图：AB,CD相交于O,∠A=∠B,

求证：∠C=∠D

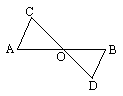
证明：∵∠A=∠B(已知)

　　  ∴AC∥BD(    )

　　  ∴∠C=∠D(    )