
题目列表(包括答案和解析)
| a |
| b |
| b |
| a |
| 1 |
| 30 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 1 |
| 30 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 1 |
| 10 |
| 1 |
| 42 |
| 1 |
| 6 |
| 3 |
| 14 |
| 2 |
| 3 |
| 2 |
| 7 |
| a |
| b |
| b |
| a |
| 1 |
| 30 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 1 |
| 30 |
| 2 |
| 3 |
| 1 |
| 10 |
| 1 |
| 6 |
| 2 |
| 5 |
| 1 |
| 10 |
| 1 |
| 42 |
| 1 |
| 6 |
| 3 |
| 14 |
| 2 |
| 3 |
| 2 |
| 7 |
 (b2-4ac≥0),显然这个一元二次方程的根的情况由b2-4ac来决定,我们把b2-4ac叫做一元二次方程ax2+bx+c=0的根的判别式,用符号“△”来表示.
(b2-4ac≥0),显然这个一元二次方程的根的情况由b2-4ac来决定,我们把b2-4ac叫做一元二次方程ax2+bx+c=0的根的判别式,用符号“△”来表示. 时,原方程有两个不相等的实数根
时,原方程有两个不相等的实数根 时,原方程有两个相等的实数根
时,原方程有两个相等的实数根 时,原方程没有实数根
时,原方程没有实数根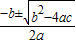 (b2-4ac≥0),显然这个一元二次方程的根的情况由b2-4ac来决定,我们把b2-4ac叫做一元二次方程ax2+bx+c=0的根的判别式,用符号“△”来表示.
(b2-4ac≥0),显然这个一元二次方程的根的情况由b2-4ac来决定,我们把b2-4ac叫做一元二次方程ax2+bx+c=0的根的判别式,用符号“△”来表示. 时,原方程有两个不相等的实数根
时,原方程有两个不相等的实数根 时,原方程有两个相等的实数根
时,原方程有两个相等的实数根 时,原方程没有实数根
时,原方程没有实数根湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com