
题目列表(包括答案和解析)
如图所示表示玲玲骑自行车离家的距离与时间的关系,她9点离开家,15点回到家,请根据图像回答下列问题:
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息多长时间?
(3)第一次休息时,离家多远?
(4)11:00到12:00她骑了多少千米?
(5)她在9:00~10:00和10:00~10:30的平均速度各是多少?
(6)她在何时至何时停止前进并休息用午餐?
(7)她在停止前进后返回,骑了多少千米?
(8)返回时的平均速度是多少?

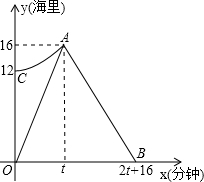 (2013•连云港)我市某海域内有一艘轮船发生故障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障渔船会合后立即将其拖回.如图折线段O-A-B表示救援船在整个航行过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律.抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律.已知救援船返程速度是前往速度的
(2013•连云港)我市某海域内有一艘轮船发生故障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障渔船会合后立即将其拖回.如图折线段O-A-B表示救援船在整个航行过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律.抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律.已知救援船返程速度是前往速度的| 2 | 3 |

| 9 | 4 |
如图11-1,是我们平时使用的等臂圆规,即CA=CB.若n个相同规格的等臂圆规的两脚依次摆放在同一条直线上如图2所示,其张角度数变化如下:∠A1C1A2=160°,∠A2C2A3=80°,∠A3C3A4=40°,∠A4C4A5=20°,…. ,根据上述规律请你写出∠AnCnAn+1=_______________°.(用含n的代数式表示)
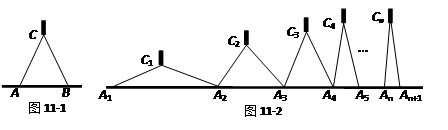
如图11-1,是我们平时使用的等臂圆规,即CA=CB.若n个相同规格的等臂圆规的两脚依次摆放在同一条直线上如图2所示,其张角度数变化如下:∠A1C1A2=160°,∠A2C2A3=80°,∠A3C3A4=40°,∠A4C4A5=20°,…. ,根据上述规律请你写出∠AnCnAn+1=_______________°.(用含n的代数式表示)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com